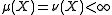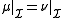Pi system
Encyclopedia
In mathematics
, a π-system on a set Ω is a set P, consisting of certain subsets of Ω, such that
That is, P is a non-empty family of subsets of Ω that is closed
under finite intersections
.
may be considered to be uniquely determined by its values on a π-system in the following sense. Let μ and υ be measures on (X, Σ) and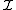
be a π-system that generates Σ. If
then μ=υ.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a π-system on a set Ω is a set P, consisting of certain subsets of Ω, such that
- P is non-empty.
- A ∩ B ∈ P whenever A and B are in P.
That is, P is a non-empty family of subsets of Ω that is closed
Closure (mathematics)
In mathematics, a set is said to be closed under some operation if performance of that operation on members of the set always produces a unique member of the same set. For example, the real numbers are closed under subtraction, but the natural numbers are not: 3 and 8 are both natural numbers, but...
under finite intersections
Intersection (set theory)
In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
.
Properties
- A σ-algebraSigma-algebraIn mathematics, a σ-algebra is a technical concept for a collection of sets satisfying certain properties. The main use of σ-algebras is in the definition of measures; specifically, the collection of sets over which a measure is defined is a σ-algebra...
is necessarily a π-system. - A π-system which is also a Dynkin systemDynkin systemA Dynkin system, named after Eugene Dynkin, is a collection of subsets of another universal set \Omega satisfying a set of axioms weaker than those of σ-algebra. Dynkin systems are sometimes referred to as λ-systems or d-system...
is a σ-algebra. - A topology is a π-system.
Uniqueness of Extension
A finite measureMeasure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
may be considered to be uniquely determined by its values on a π-system in the following sense. Let μ and υ be measures on (X, Σ) and
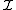be a π-system that generates Σ. If
then μ=υ.