
Perfect spline
Encyclopedia
In the mathematical subfields function theory and numerical analysis
, a univariate polynomial spline
of order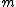 is called a perfect spline if its
is called a perfect spline if its 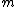 -th derivative is equal to
-th derivative is equal to 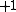 or
or 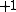 between knots and changes its sign at every knot.
between knots and changes its sign at every knot.
The term was coined by Isaac Jacob Schoenberg
.
Perfect splines often give solutions to various extremal problems in mathematics. For example norms
of periodic perfect splines (they are sometimes called Euler perfect splines) are equal to Favard's constants.
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
, a univariate polynomial spline
Spline (mathematics)
In mathematics, a spline is a sufficiently smooth piecewise-polynomial function. In interpolating problems, spline interpolation is often preferred to polynomial interpolation because it yields similar results, even when using low-degree polynomials, while avoiding Runge's phenomenon for higher...
of order
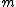 is called a perfect spline if its
is called a perfect spline if its 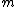 -th derivative is equal to
-th derivative is equal to 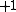 or
or 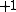 between knots and changes its sign at every knot.
between knots and changes its sign at every knot.The term was coined by Isaac Jacob Schoenberg
Isaac Jacob Schoenberg
Isaac Jacob Schoenberg was a Romanian mathematician, known for his discovery of splines.He studied at the University of Iaşi, receiving his M.A. in 1922. From 1922 to 1925 he studied at the Universities of Berlin and Göttingen, working on a topic in analytic number theory suggested by Issai Schur...
.
Perfect splines often give solutions to various extremal problems in mathematics. For example norms
Norm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
of periodic perfect splines (they are sometimes called Euler perfect splines) are equal to Favard's constants.

