Paterson's worms
Encyclopedia
Paterson's Worms are a family of Turing machine
s devised in 1971 by Mike Paterson
and John Horton Conway
to model the behaviour and feeding patterns of certain prehistoric worms. In the model, a worm moves between points on a triangular grid along line segments, representing food. Its turnings are determined by the configuration of eaten and uneaten line segments adjacent to the point the worm is currently on. Despite being governed by simple rules the behaviour of the worms can be extremely complex, and the ultimate fate of two variants is still unknown.
The Worms were studied in the early 1970s by Paterson, Conway and Michael Beeler, described by Beeler in June 1973 MIT AI Memo
#290: "Paterson's Worm", and presented in November 1973 in Martin Gardner
's "Mathematical Games" column in Scientific American
.
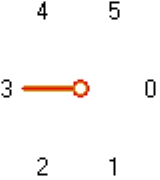
The six directions are numbered as follows:
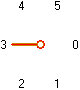
So direction 0 indicates the worm continues to travel straight ahead, direction 1 indicates the worm will make a right turn of 60 and similarly for the other directions. The worm cannot travel in direction 3 because that is the gridline it has just traversed. Thus a worm with rule {1,0,5,1} decides to travel in direction 1 the first time it has to make a choice, in direction 0 the next time it has to make a choice and so on. If there is only one available gridline, the worm has no choice but to take it and this is usually not explicitly listed.
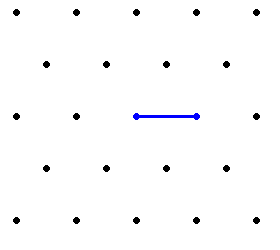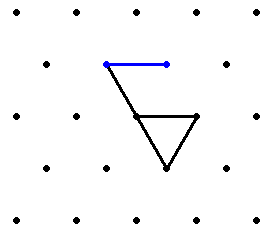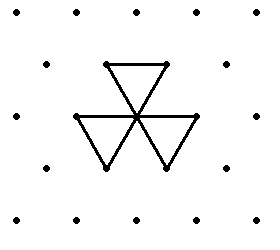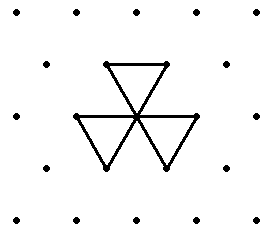A worm whose ruleset begins with 0 continues in a straight line forever. This is a trivial case, so it is usually stipulated that the worm must turn when it encounters a point with only uneaten gridlines. Furthermore, to avoid mirror-image symmetrical duplicates, the worm's first turn must be a right hand turn. A worm dies if it returns to its origin a third time, because there are then no untraversed edges available. Only the origin can be lethal to the worm.
There are 411 different species of worm (412 if the infinite straight-line worm is included), of which 336 eventually die. 73 patterns exhibit infinite behaviour, that is, they settle into a repeating pattern that does not return to the origin. A further two are strongly believed to be infinite and one remains unsolved. Eleven of the rules exhibit complicated behaviour. They do not die even after many billions of iterations, nor do they adopt an obviously infinite pattern. Their ultimate fate was unknown until 2003 when Benjamin Chaffin developed new methods of solving them. After many hours of computer time, nine of the eleven rules were solved, leaving the worms with rules {1,0,4,2,0,2,0} and {1,0,4,2,0,1,5}. The first of these was solved by Tomas Rokicki, who determined that it halts after 57 trillion timesteps, leaving only {1,0,4,2,0,1,5} unsolved. According to Rokicki, the worm is still active after 5.2×1019 timesteps. He used an algorithm based on Bill Gosper
's Hashlife
to simulate the worms at extraordinary speeds.
Certain species of prehistoric worms fed upon sediment at the bottom of ponds. These worms avoided retracing paths they had already travelled because food would be scarce there but, because food occurred in patches, it was in the worm's interest to stay near previous trails. Different species of worm had different innate rules regarding how close to travelled paths to stay, when to turn and how sharp a turn to make. In 1969 Raup and Seilacher
created computer simulations of the fossilized worm trails, and these simulations inspired Paterson and Conway to develop a simple set of rules to study idealized worms on regular grids.
Conway's original model was a worm on an orthogonal grid but this produced only three different species of worm, all with rather uninteresting behaviour. Paterson considered worms on a triangular grid. Paterson's Worms were presented in November 1973 in Martin Gardner
's "Mathematical Games" column in Scientific American
, reprinted in .
Turing machine
A Turing machine is a theoretical device that manipulates symbols on a strip of tape according to a table of rules. Despite its simplicity, a Turing machine can be adapted to simulate the logic of any computer algorithm, and is particularly useful in explaining the functions of a CPU inside a...
s devised in 1971 by Mike Paterson
Mike Paterson
Michael Stewart "Mike" Paterson, is the director of the Centre for Discrete Mathematics and its Applications in the Department of Computer Science at the University of Warwick, and was chair of that department in 2005....
and John Horton Conway
John Horton Conway
John Horton Conway is a prolific mathematician active in the theory of finite groups, knot theory, number theory, combinatorial game theory and coding theory...
to model the behaviour and feeding patterns of certain prehistoric worms. In the model, a worm moves between points on a triangular grid along line segments, representing food. Its turnings are determined by the configuration of eaten and uneaten line segments adjacent to the point the worm is currently on. Despite being governed by simple rules the behaviour of the worms can be extremely complex, and the ultimate fate of two variants is still unknown.
The Worms were studied in the early 1970s by Paterson, Conway and Michael Beeler, described by Beeler in June 1973 MIT AI Memo
AI Memo
The AI Memos are a series of influential memorandums and technical reports published by the MIT AI Lab, Massachusetts Institute of Technology, USA...
#290: "Paterson's Worm", and presented in November 1973 in Martin Gardner
Martin Gardner
Martin Gardner was an American mathematics and science writer specializing in recreational mathematics, but with interests encompassing micromagic, stage magic, literature , philosophy, scientific skepticism, and religion...
's "Mathematical Games" column in Scientific American
Scientific American
Scientific American is a popular science magazine. It is notable for its long history of presenting science monthly to an educated but not necessarily scientific public, through its careful attention to the clarity of its text as well as the quality of its specially commissioned color graphics...
.
Rules
The worm starts at some point of an infinite triangular grid. It starts moving along one of the six gridlines and, once it has travelled one unit of distance, it arrives at a new point. The worm then decides, based on the distribution of traversed and untraversed gridlines, what direction it will take. The directions are relative to the worm's point of view. If the worm has not encountered this exact distribution before it may leave along any untraversed gridline. From then on, if it encounters that distribution again, it must move in the same way. If there are no untraversed gridlines available, the worm dies and the simulation ends.Discussion
There are many different types of worm depending on which direction they turn when encountering a new type of intersection. The different varieties of worm can be classified systematically by assigning every direction a number and listing the choice made every time a new type of intersection is encountered.The six directions are numbered as follows:
So direction 0 indicates the worm continues to travel straight ahead, direction 1 indicates the worm will make a right turn of 60 and similarly for the other directions. The worm cannot travel in direction 3 because that is the gridline it has just traversed. Thus a worm with rule {1,0,5,1} decides to travel in direction 1 the first time it has to make a choice, in direction 0 the next time it has to make a choice and so on. If there is only one available gridline, the worm has no choice but to take it and this is usually not explicitly listed.
There are 411 different species of worm (412 if the infinite straight-line worm is included), of which 336 eventually die. 73 patterns exhibit infinite behaviour, that is, they settle into a repeating pattern that does not return to the origin. A further two are strongly believed to be infinite and one remains unsolved. Eleven of the rules exhibit complicated behaviour. They do not die even after many billions of iterations, nor do they adopt an obviously infinite pattern. Their ultimate fate was unknown until 2003 when Benjamin Chaffin developed new methods of solving them. After many hours of computer time, nine of the eleven rules were solved, leaving the worms with rules {1,0,4,2,0,2,0} and {1,0,4,2,0,1,5}. The first of these was solved by Tomas Rokicki, who determined that it halts after 57 trillion timesteps, leaving only {1,0,4,2,0,1,5} unsolved. According to Rokicki, the worm is still active after 5.2×1019 timesteps. He used an algorithm based on Bill Gosper
Bill Gosper
Ralph William Gosper, Jr. , known as Bill Gosper, is an American mathematician and programmer from Pennsauken Township, New Jersey...
's Hashlife
Hashlife
Hashlife is a memoized algorithm for computing the long-term fate of a given starting configuration in Conway's Game of Life and related cellular automata, much more quickly than would be possible using alternative algorithms that simulate each time step of each cell of the automaton...
to simulate the worms at extraordinary speeds.
History
Adolf Seilacher
Adolf "Dolf" Seilacher is a German palaeontologist who has made major contributions to evolutionary and ecological palaeobiology in a career stretching over 60 years. He won the Crafoord Prize in 1992, the Paleontological Society Medal in 1994 and the Palaeontological Association's Lapworth Medal...
created computer simulations of the fossilized worm trails, and these simulations inspired Paterson and Conway to develop a simple set of rules to study idealized worms on regular grids.
Conway's original model was a worm on an orthogonal grid but this produced only three different species of worm, all with rather uninteresting behaviour. Paterson considered worms on a triangular grid. Paterson's Worms were presented in November 1973 in Martin Gardner
Martin Gardner
Martin Gardner was an American mathematics and science writer specializing in recreational mathematics, but with interests encompassing micromagic, stage magic, literature , philosophy, scientific skepticism, and religion...
's "Mathematical Games" column in Scientific American
Scientific American
Scientific American is a popular science magazine. It is notable for its long history of presenting science monthly to an educated but not necessarily scientific public, through its careful attention to the clarity of its text as well as the quality of its specially commissioned color graphics...
, reprinted in .