
Partially observable Markov decision process
Encyclopedia
A Partially Observable Markov Decision Process (POMDP) is a generalization of a Markov Decision Process
. A POMDP models an agent decision process in which it is assumed that the system dynamics are determined by an MDP, but the agent cannot directly observe the underlying state. Instead, it must maintain a probability distribution over the set of possible states, based on a set of observations and observation probabilities, and the underlying MDP.
The POMDP framework is general enough to model a variety of real-world sequential decision processes. Applications include robot navigation problems, machine maintenance, and planning under uncertainty in general. The framework originated in the Operations Research community, and was later taken over by the Artificial Intelligence
and Automated Planning communities.
An exact solution to a POMDP yields the optimal action for each possible belief over the world states. The optimal action maximizes (or minimizes) the expected reward (or cost) of the agent over a possibly infinite horizon. The sequence of optimal actions is known as the optimal policy of the agent for interacting with its environment.
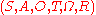 , where
, where
At each time period, the environment is in some state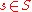 . The agent takes an action
. The agent takes an action 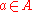 ,
,
which causes the environment to transition to state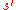 with probability
with probability 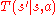 . Finally, the agent receives a reward with expected value
. Finally, the agent receives a reward with expected value 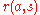 , and the process repeats. The difficulty is that the agent does not know the exact state
, and the process repeats. The difficulty is that the agent does not know the exact state  . Instead, it must maintain a probability distribution, known as the belief state, over the possible states
. Instead, it must maintain a probability distribution, known as the belief state, over the possible states 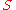 .
.
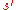 , the agent observes
, the agent observes  with probability
with probability 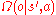 . Let
. Let  be a probability distribution over the state space
be a probability distribution over the state space 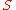 :
: 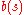 denotes the probability that the environment is in state
denotes the probability that the environment is in state  . Given
. Given 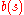 , then after taking action
, then after taking action  and observing
and observing  ,
,
where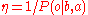 is a normalizing constant with
is a normalizing constant with 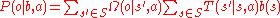 .
.
Since the state is Markovian, maintaining a belief over the states solely requires knowledge of the previous belief state, the action taken, and the current observation. The operation is denoted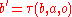 .
.
(MDP). It is defined as a tuple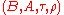 where
where
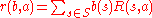 .
.
Note that this MDP is defined over a continuous state space.
 specifies an action
specifies an action  for any belief
for any belief  . Here it is assumed the objective is to maximize the expected total discounted reward over an infinite horizon. When
. Here it is assumed the objective is to maximize the expected total discounted reward over an infinite horizon. When  defines a cost, the objective becomes the minimization of the expected cost.
defines a cost, the objective becomes the minimization of the expected cost.
The expected reward for policy starting from belief
starting from belief  is defined as
is defined as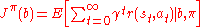
where is the discount factor. The optimal policy
is the discount factor. The optimal policy  is obtained by optimizing the long-term reward.
is obtained by optimizing the long-term reward.
where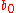 is the initial belief.
is the initial belief.
The optimal policy, noted yields the highest expected reward value for each belief state, compactly represented by the optimal value function, noted
yields the highest expected reward value for each belief state, compactly represented by the optimal value function, noted 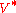 . This value function is solution to the Bellman optimality equation
. This value function is solution to the Bellman optimality equation
: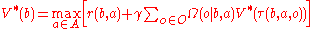
For finite-horizon POMDPs, the optimal value function is piecewise-linear and convex. It can be represented as a finite set of vectors. In the infinite-horizon formulation, a finite vector set can approximate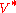 arbitrarily closely, whose shape remains convex. Value iteration applies dynamic programming update to gradually improve on the value until convergence to an
arbitrarily closely, whose shape remains convex. Value iteration applies dynamic programming update to gradually improve on the value until convergence to an  -optimal value function, and preserves its piecewise linearity and convexity. By improving the value, the policy is implicitly improved. Another dynamic programming technique called policy iteration explicitly represents and improves the policy instead.
-optimal value function, and preserves its piecewise linearity and convexity. By improving the value, the policy is implicitly improved. Another dynamic programming technique called policy iteration explicitly represents and improves the policy instead.
Grid-based algorithms comprise one approximate solution technique. In this approach, the value function is computed for a set of points in the belief space, and interpolation is used to determine the optimal action to take for other belief states that are encountered and that aren't in the set of grid points. More recent work makes use of sampling techniques, generalization techniques and exploitation of problem structure, and has extended POMDP solving into large domains with millions of states For example, point-based methods sample random reachable belief points to constrain the planning to relevant areas in the belief space.
Dimensionality reduction using PCA has also been explored.
Markov decision process
Markov decision processes , named after Andrey Markov, provide a mathematical framework for modeling decision-making in situations where outcomes are partly random and partly under the control of a decision maker. MDPs are useful for studying a wide range of optimization problems solved via...
. A POMDP models an agent decision process in which it is assumed that the system dynamics are determined by an MDP, but the agent cannot directly observe the underlying state. Instead, it must maintain a probability distribution over the set of possible states, based on a set of observations and observation probabilities, and the underlying MDP.
The POMDP framework is general enough to model a variety of real-world sequential decision processes. Applications include robot navigation problems, machine maintenance, and planning under uncertainty in general. The framework originated in the Operations Research community, and was later taken over by the Artificial Intelligence
Artificial intelligence
Artificial intelligence is the intelligence of machines and the branch of computer science that aims to create it. AI textbooks define the field as "the study and design of intelligent agents" where an intelligent agent is a system that perceives its environment and takes actions that maximize its...
and Automated Planning communities.
An exact solution to a POMDP yields the optimal action for each possible belief over the world states. The optimal action maximizes (or minimizes) the expected reward (or cost) of the agent over a possibly infinite horizon. The sequence of optimal actions is known as the optimal policy of the agent for interacting with its environment.
Formal Definition
A discrete-time POMDP models the relationship between an agent and its environment. Formally, a POMDP is a tuple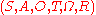 , where
, where
-
 is a set of states,
is a set of states, -
 is a set of actions,
is a set of actions, -
 is a set of observations,
is a set of observations, -
 is a set of conditional transition probabilities,
is a set of conditional transition probabilities, -
 is a set of conditional observation probabilities,
is a set of conditional observation probabilities, -
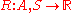 is the reward function.
is the reward function.
At each time period, the environment is in some state
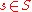 . The agent takes an action
. The agent takes an action 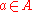 ,
,which causes the environment to transition to state
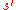 with probability
with probability 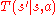 . Finally, the agent receives a reward with expected value
. Finally, the agent receives a reward with expected value 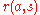 , and the process repeats. The difficulty is that the agent does not know the exact state
, and the process repeats. The difficulty is that the agent does not know the exact state  . Instead, it must maintain a probability distribution, known as the belief state, over the possible states
. Instead, it must maintain a probability distribution, known as the belief state, over the possible states 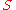 .
.Belief update
In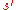 , the agent observes
, the agent observes  with probability
with probability 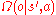 . Let
. Let  be a probability distribution over the state space
be a probability distribution over the state space 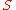 :
: 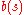 denotes the probability that the environment is in state
denotes the probability that the environment is in state  . Given
. Given 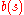 , then after taking action
, then after taking action  and observing
and observing  ,
,
where
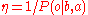 is a normalizing constant with
is a normalizing constant with 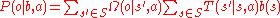 .
.Since the state is Markovian, maintaining a belief over the states solely requires knowledge of the previous belief state, the action taken, and the current observation. The operation is denoted
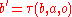 .
.Belief MDP
The policy maps a belief state space into the action space. The optimal policy can be understood as the solution of a continuous space so-called belief Markov Decision ProcessMarkov decision process
Markov decision processes , named after Andrey Markov, provide a mathematical framework for modeling decision-making in situations where outcomes are partly random and partly under the control of a decision maker. MDPs are useful for studying a wide range of optimization problems solved via...
(MDP). It is defined as a tuple
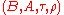 where
where
-
 is the set of belief states over the POMDP states,
is the set of belief states over the POMDP states, -
 is the same finite set of action as for the original POMDP,
is the same finite set of action as for the original POMDP, -
 is the belief state transition function,
is the belief state transition function, -
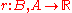 is the reward function on belief states. It writes :
is the reward function on belief states. It writes :
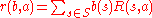 .
.Note that this MDP is defined over a continuous state space.
Policy and Value Function
The agent's policy specifies an action
specifies an action  for any belief
for any belief  . Here it is assumed the objective is to maximize the expected total discounted reward over an infinite horizon. When
. Here it is assumed the objective is to maximize the expected total discounted reward over an infinite horizon. When  defines a cost, the objective becomes the minimization of the expected cost.
defines a cost, the objective becomes the minimization of the expected cost.The expected reward for policy
 starting from belief
starting from belief  is defined as
is defined as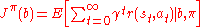
where
 is the discount factor. The optimal policy
is the discount factor. The optimal policy  is obtained by optimizing the long-term reward.
is obtained by optimizing the long-term reward.
where
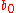 is the initial belief.
is the initial belief.The optimal policy, noted
 yields the highest expected reward value for each belief state, compactly represented by the optimal value function, noted
yields the highest expected reward value for each belief state, compactly represented by the optimal value function, noted 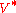 . This value function is solution to the Bellman optimality equation
. This value function is solution to the Bellman optimality equationBellman equation
A Bellman equation , named after its discoverer, Richard Bellman, is a necessary condition for optimality associated with the mathematical optimization method known as dynamic programming...
:
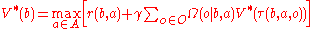
For finite-horizon POMDPs, the optimal value function is piecewise-linear and convex. It can be represented as a finite set of vectors. In the infinite-horizon formulation, a finite vector set can approximate
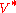 arbitrarily closely, whose shape remains convex. Value iteration applies dynamic programming update to gradually improve on the value until convergence to an
arbitrarily closely, whose shape remains convex. Value iteration applies dynamic programming update to gradually improve on the value until convergence to an  -optimal value function, and preserves its piecewise linearity and convexity. By improving the value, the policy is implicitly improved. Another dynamic programming technique called policy iteration explicitly represents and improves the policy instead.
-optimal value function, and preserves its piecewise linearity and convexity. By improving the value, the policy is implicitly improved. Another dynamic programming technique called policy iteration explicitly represents and improves the policy instead.Approximate POMDP solutions
In practice, POMDPs are often computationally intractable to solve exactly, so computer scientists have developed methods that approximate solutions for POMDPs.Grid-based algorithms comprise one approximate solution technique. In this approach, the value function is computed for a set of points in the belief space, and interpolation is used to determine the optimal action to take for other belief states that are encountered and that aren't in the set of grid points. More recent work makes use of sampling techniques, generalization techniques and exploitation of problem structure, and has extended POMDP solving into large domains with millions of states For example, point-based methods sample random reachable belief points to constrain the planning to relevant areas in the belief space.
Dimensionality reduction using PCA has also been explored.
POMDP uses
POMDPs model many kinds of real-world problems. Notable works include the use of a POMDP in assistive technology for persons with dementia and the conservation of the critically endangered and difficult to detect Sumatran tigers.External links
- Tony Cassandra's POMDP pages with a tutorial, examples of problems modeled as POMDPs, and software for solving them.
- zmdp, a POMDP solver by Trey Smith
- APPL, a fast point-based POMDP solver
- SPUDD, a factored structured (PO)MDP solver that uses algebraic decision diagrams (ADDs).

