
Pair distribution function
Encyclopedia
The pair distribution function (PDF) describes the distribution of distances between pairs of particles contained within a given volume. Mathematically, if a and b are two particles in a fluid, the PDF of b with respect to a, denoted by 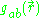 is the probability of finding the particle b at the distance
is the probability of finding the particle b at the distance  from a, with a taken as the origin of coordinates.
from a, with a taken as the origin of coordinates.
 :
: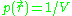 ,
,
where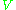 is the volume of the container. On the other hand, the likelihood of finding pairs of objects at given positions (i.e. the two-body probability density) is not uniform. For example, pairs of hard balls must be separated by at least the diameter of a ball. The pair distribution function
is the volume of the container. On the other hand, the likelihood of finding pairs of objects at given positions (i.e. the two-body probability density) is not uniform. For example, pairs of hard balls must be separated by at least the diameter of a ball. The pair distribution function  is obtained by scaling the two-body probability density function by the total number of objects
is obtained by scaling the two-body probability density function by the total number of objects 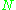 and the size of the container:
and the size of the container: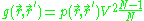 .
.
In the common case where the number of objects in the container is large, this simplifies to give: .
.
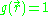 ,
,
where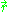 is the separation between a pair of objects. However, this is inaccurate in the case of hard objects as discussed above, because it does not account for the minimum separation required between objects. The hole-correction (HC) approximation provides a better model:
is the separation between a pair of objects. However, this is inaccurate in the case of hard objects as discussed above, because it does not account for the minimum separation required between objects. The hole-correction (HC) approximation provides a better model: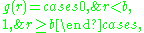
where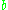 is the diameter of one of the objects.
is the diameter of one of the objects.
Although the HC approximation gives a reasonable description of sparsely packed objects, it breaks down for dense packing. This may be illustrated by considering a box completely filled by identical hard balls so that each ball touches its neighbours. In this case, every pair of balls in the box is separated by a distance of exactly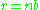 where
where  is a positive whole number. The pair distribution for a volume completely filled by hard spheres is therefore a set of delta functions of the form:
is a positive whole number. The pair distribution for a volume completely filled by hard spheres is therefore a set of delta functions of the form: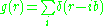 .
.
Finally, it may be noted that a pair of objects which are separated by a large distance have no influence on each other's position (provided that the container is not completely filled). Therefore,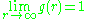 .
.
In general, a pair distribution function will take a form somewhere between the sparsely packed (HC approximation) and the densely packed (delta function) models, depending on the packing density .
.
or x-ray powder diffraction through the use of Fourier Transform
.
In Statistical Mechanics the PDF is given by the expression:
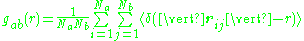
The Diffpy project is used to match crystal structures with PDF data derived from X-ray or neutron diffraction data.
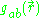 is the probability of finding the particle b at the distance
is the probability of finding the particle b at the distance 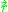 from a, with a taken as the origin of coordinates.
from a, with a taken as the origin of coordinates.Overview
The pair distribution function is used to describe the distribution of a objects within a medium (for example, oranges in a crate or nitrogen molecules in a gas cylinder). If the medium is homogeneous (i.e. every spatial location has identical properties), then there is an equal probability density for finding an object at any position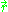 :
: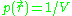 ,
,where
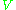 is the volume of the container. On the other hand, the likelihood of finding pairs of objects at given positions (i.e. the two-body probability density) is not uniform. For example, pairs of hard balls must be separated by at least the diameter of a ball. The pair distribution function
is the volume of the container. On the other hand, the likelihood of finding pairs of objects at given positions (i.e. the two-body probability density) is not uniform. For example, pairs of hard balls must be separated by at least the diameter of a ball. The pair distribution function  is obtained by scaling the two-body probability density function by the total number of objects
is obtained by scaling the two-body probability density function by the total number of objects 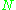 and the size of the container:
and the size of the container: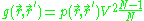 .
.In the common case where the number of objects in the container is large, this simplifies to give:
 .
.Simple models and general properties
The simplest possible pair distribution function assumes that all object locations are mutually independent, giving: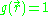 ,
,where
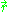 is the separation between a pair of objects. However, this is inaccurate in the case of hard objects as discussed above, because it does not account for the minimum separation required between objects. The hole-correction (HC) approximation provides a better model:
is the separation between a pair of objects. However, this is inaccurate in the case of hard objects as discussed above, because it does not account for the minimum separation required between objects. The hole-correction (HC) approximation provides a better model: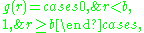
where
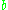 is the diameter of one of the objects.
is the diameter of one of the objects.Although the HC approximation gives a reasonable description of sparsely packed objects, it breaks down for dense packing. This may be illustrated by considering a box completely filled by identical hard balls so that each ball touches its neighbours. In this case, every pair of balls in the box is separated by a distance of exactly
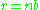 where
where  is a positive whole number. The pair distribution for a volume completely filled by hard spheres is therefore a set of delta functions of the form:
is a positive whole number. The pair distribution for a volume completely filled by hard spheres is therefore a set of delta functions of the form: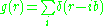 .
.Finally, it may be noted that a pair of objects which are separated by a large distance have no influence on each other's position (provided that the container is not completely filled). Therefore,
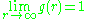 .
.In general, a pair distribution function will take a form somewhere between the sparsely packed (HC approximation) and the densely packed (delta function) models, depending on the packing density
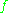 .
.Radial pair distributions
Of special practical importance is the radial pair distribution function, which is independent of orientation. It is a major descriptor for the atomic structure of amorphous materials (glasses, polymers) and liquids. The radial PDF can be calculated directly from physical measurements like light scatteringLight scattering
Light scattering is a form of scattering in which light is the form of propagating energy which is scattered. Light scattering can be thought of as the deflection of a ray from a straight path, for example by irregularities in the propagation medium, particles, or in the interface between two media...
or x-ray powder diffraction through the use of Fourier Transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
.
In Statistical Mechanics the PDF is given by the expression:
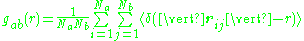
The Diffpy project is used to match crystal structures with PDF data derived from X-ray or neutron diffraction data.

