
P-adic exponential function
Encyclopedia
In mathematics
, particularly p-adic analysis
, the p-adic exponential function is a p-adic analogue of the usual exponential function
on the complex numbers. As in the complex case, it has an inverse function named the p-adic logarithm.
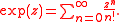
Entirely analogously, one defines the exponential function on Cp, the completion of the algebraic closure of Qp, by
However, unlike exp which converges on all of C, expp only converges on the disc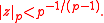
This is because p-adic series converge if and only if the summands tend to zero, and since the n! in the denominator of each summand tends to make them very large p-adically, rather a small value of z is needed in the numerator.
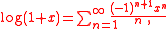
converges for x in Cp satisfying |x|p < 1 and so defines the p-adic logarithm function logp(z) for |z − 1|p < 1 satisfying the usual property logp(zw) = logpz + logpw. The function logp can be extended to all of (the set of nonzero elements of Cp) by imposing that it continue to satisfy this last property and setting logp(p) = 0. Specifically, every element w of can be written as w = pr·ζ·z with r a rational number, ζ a root of unity, and |z − 1|p < 1, in which case logp(w) = logp(z). This function on is sometimes called the Iwasawa logarithm to emphasize the choice of logp(p) = 0. In fact, there is an extension of the logarithm from |z − 1|p < 1 to all of for each choice of logp(p) in Cp.
Similarly if z and w are nonzero elements of Cp then logp(zw) = logpz + logpw.
And for suitable z, so that everything is defined, we have expp(logp(z)) = z and logp(expp(z)) = z.
The roots of the Iwasawa logarithm logp(z) are exactly the elements of Cp of the form pr·ζ where r is a rational number and ζ is a root of unity.
Note that there is no analogue in Cp of Euler's identity, e2πi = 1. This is a corollary of Strassmann's theorem
.
Another major difference to the situation in C is that the domain of convergence of expp is much smaller than that of logp. A modified exponential function — the Artin–Hasse exponential — can be used instead which converges on |z|p < 1.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, particularly p-adic analysis
P-adic analysis
In mathematics, p-adic analysis is a branch of number theory that deals with the mathematical analysis of functions of p-adic numbers....
, the p-adic exponential function is a p-adic analogue of the usual exponential function
Exponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
on the complex numbers. As in the complex case, it has an inverse function named the p-adic logarithm.
Definition
The usual exponential function on C is defined by the infinite series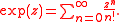
Entirely analogously, one defines the exponential function on Cp, the completion of the algebraic closure of Qp, by

However, unlike exp which converges on all of C, expp only converges on the disc
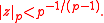
This is because p-adic series converge if and only if the summands tend to zero, and since the n! in the denominator of each summand tends to make them very large p-adically, rather a small value of z is needed in the numerator.
p-adic logarithm function
The power series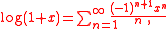
converges for x in Cp satisfying |x|p < 1 and so defines the p-adic logarithm function logp(z) for |z − 1|p < 1 satisfying the usual property logp(zw) = logpz + logpw. The function logp can be extended to all of (the set of nonzero elements of Cp) by imposing that it continue to satisfy this last property and setting logp(p) = 0. Specifically, every element w of can be written as w = pr·ζ·z with r a rational number, ζ a root of unity, and |z − 1|p < 1, in which case logp(w) = logp(z). This function on is sometimes called the Iwasawa logarithm to emphasize the choice of logp(p) = 0. In fact, there is an extension of the logarithm from |z − 1|p < 1 to all of for each choice of logp(p) in Cp.
Properties
If z and w are both in the radius of convergence for expp, then their sum is too and we have the usual addition formula: expp(z + w) = expp(z)expp(w).Similarly if z and w are nonzero elements of Cp then logp(zw) = logpz + logpw.
And for suitable z, so that everything is defined, we have expp(logp(z)) = z and logp(expp(z)) = z.
The roots of the Iwasawa logarithm logp(z) are exactly the elements of Cp of the form pr·ζ where r is a rational number and ζ is a root of unity.
Note that there is no analogue in Cp of Euler's identity, e2πi = 1. This is a corollary of Strassmann's theorem
Strassmann's theorem
In mathematics, Strassman's theorem is a result in field theory introduced by . It states that, for suitable fields, suitable formal power series with coefficients in the valuation ring of the field have only finitely many zeroes.-Statement of the theorem:...
.
Another major difference to the situation in C is that the domain of convergence of expp is much smaller than that of logp. A modified exponential function — the Artin–Hasse exponential — can be used instead which converges on |z|p < 1.

