
Overlapping interval topology
Encyclopedia
In mathematics
, the overlapping interval topology is a topology
which is used to illustrate various topological principles.
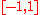 of the real number line, the open set
of the real number line, the open set
s of the topology are generated
from the half-open intervals and
and 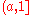 with
with 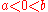 . The topology therefore consists of intervals of the form
. The topology therefore consists of intervals of the form  ,
, 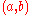 , and
, and 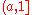 with
with 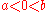 , together with
, together with 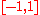 itself and the empty set.
itself and the empty set.
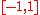 are topologically distinguishable under the overlapping interval topology as one can always find an open set containing one but not the other point. However, every non-empty open set contains the point 0 which can therefore not be separated from any other point in
are topologically distinguishable under the overlapping interval topology as one can always find an open set containing one but not the other point. However, every non-empty open set contains the point 0 which can therefore not be separated from any other point in 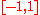 , making
, making 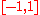 with the overlapping interval topology an example of a T0 space that is not a T1 space
with the overlapping interval topology an example of a T0 space that is not a T1 space
.
The overlapping interval topology is second countable, with a countable basis being given by the intervals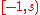 ,
, 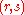 and
and 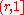 with
with  and r and s rational (and thus countable).
and r and s rational (and thus countable).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the overlapping interval topology is a topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
which is used to illustrate various topological principles.
Definition
Given the closed interval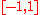 of the real number line, the open set
of the real number line, the open setOpen set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
s of the topology are generated
Subbase
In topology, a subbase for a topological space X with topology T is a subcollection B of T which generates T, in the sense that T is the smallest topology containing B...
from the half-open intervals
 and
and 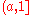 with
with 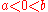 . The topology therefore consists of intervals of the form
. The topology therefore consists of intervals of the form  ,
, 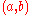 , and
, and 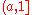 with
with 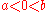 , together with
, together with 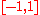 itself and the empty set.
itself and the empty set.Properties
Any two distinct points in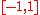 are topologically distinguishable under the overlapping interval topology as one can always find an open set containing one but not the other point. However, every non-empty open set contains the point 0 which can therefore not be separated from any other point in
are topologically distinguishable under the overlapping interval topology as one can always find an open set containing one but not the other point. However, every non-empty open set contains the point 0 which can therefore not be separated from any other point in 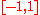 , making
, making 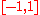 with the overlapping interval topology an example of a T0 space that is not a T1 space
with the overlapping interval topology an example of a T0 space that is not a T1 spaceT1 space
In topology and related branches of mathematics, a T1 space is a topological space in which, for every pair of distinct points, each has an open neighborhood not containing the other. An R0 space is one in which this holds for every pair of topologically distinguishable points...
.
The overlapping interval topology is second countable, with a countable basis being given by the intervals
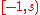 ,
, 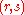 and
and 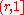 with
with  and r and s rational (and thus countable).
and r and s rational (and thus countable).

