
Overlap-save method
Encyclopedia
Overlap–save is the traditional name for an efficient way to evaluate the discrete convolution between a very long signal 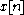 and a finite impulse response
and a finite impulse response
(FIR) filter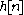 :
:
where h[m]=0 for m outside the region [1, M].
The concept is to compute short segments of y[n] of an arbitrary length L, and concatenate the segments together. Consider a segment that begins at n = kL + M, for any integer k, and define:
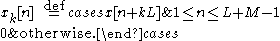
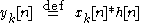
Then, for kL + M ≤ n ≤ kL + L + M − 1, and equivalently M ≤ n − kL ≤ L + M − 1, we can write:
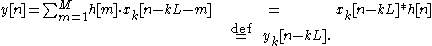
The task is thereby reduced to computing yk[n], for M ≤ n ≤ L + M − 1.
Now note that if we periodically extend xk[n] with period N ≥ L + M − 1, according to:

the convolutions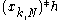 and
and 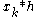 are equivalent in the region M ≤ n ≤ L + M − 1. So it is sufficient to compute the
are equivalent in the region M ≤ n ≤ L + M − 1. So it is sufficient to compute the 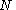 -point circular (or cyclic) convolution
-point circular (or cyclic) convolution
of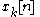 with
with 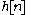 in the region [1, N]. The subregion [M, L + M − 1] is appended to the output stream, and the other values are discarded.
in the region [1, N]. The subregion [M, L + M − 1] is appended to the output stream, and the other values are discarded.
The advantage is that the circular convolution can be computed very efficiently as follows, according to the circular convolution theorem:
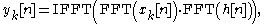
where FFT and IFFT refer to the fast Fourier transform and inverse fast Fourier transform, respectively, evaluated over N discrete points.
H = FFT(h,N)
i = 1
while i <= Nx
il = min(i+N-1,Nx)
yt = IFFT( FFT(x(i:il),N) * H, N)
y(i : i+N-M) = yt(M : N)
i = i+N-M+1
end
For example, when M=201 and N=1024, equals 26, whereas direct evaluation of would require up to 201 complex multiplications per output sample, the worst case being when both x and h are complex-valued. Also note that for any given M, has a minimum with respect to N. It diverges for both small and large block sizes.
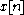 and a finite impulse response
and a finite impulse responseFinite impulse response
A finite impulse response filter is a type of a signal processing filter whose impulse response is of finite duration, because it settles to zero in finite time. This is in contrast to infinite impulse response filters, which have internal feedback and may continue to respond indefinitely...
(FIR) filter
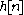 :
:where h[m]=0 for m outside the region [1, M].
The concept is to compute short segments of y[n] of an arbitrary length L, and concatenate the segments together. Consider a segment that begins at n = kL + M, for any integer k, and define:
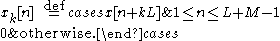
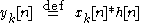
Then, for kL + M ≤ n ≤ kL + L + M − 1, and equivalently M ≤ n − kL ≤ L + M − 1, we can write:
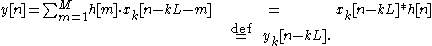
The task is thereby reduced to computing yk[n], for M ≤ n ≤ L + M − 1.
Now note that if we periodically extend xk[n] with period N ≥ L + M − 1, according to:

the convolutions
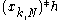 and
and 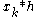 are equivalent in the region M ≤ n ≤ L + M − 1. So it is sufficient to compute the
are equivalent in the region M ≤ n ≤ L + M − 1. So it is sufficient to compute the 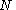 -point circular (or cyclic) convolution
-point circular (or cyclic) convolutionCircular convolution
The circular convolution, also known as cyclic convolution, of two aperiodic functions occurs when one of them is convolved in the normal way with a periodic summation of the other function. That situation arises in the context of the Circular convolution theorem...
of
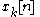 with
with 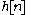 in the region [1, N]. The subregion [M, L + M − 1] is appended to the output stream, and the other values are discarded.
in the region [1, N]. The subregion [M, L + M − 1] is appended to the output stream, and the other values are discarded.The advantage is that the circular convolution can be computed very efficiently as follows, according to the circular convolution theorem:
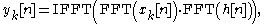
where FFT and IFFT refer to the fast Fourier transform and inverse fast Fourier transform, respectively, evaluated over N discrete points.
Pseudocode
(Overlap–save algorithm for linear convolution)H = FFT(h,N)
i = 1
while i <= Nx
il = min(i+N-1,Nx)
yt = IFFT( FFT(x(i:il),N) * H, N)
y(i : i+N-M) = yt(M : N)
i = i+N-M+1
end
Efficiency
The pseudocode above requires about 2N log2(N) + N complex multiplications for the FFT, product of arrays, and IFFT. Each iteration produces N-M+1 output samples, so the number of complex multiplications per output sample is about:For example, when M=201 and N=1024, equals 26, whereas direct evaluation of would require up to 201 complex multiplications per output sample, the worst case being when both x and h are complex-valued. Also note that for any given M, has a minimum with respect to N. It diverges for both small and large block sizes.
Overlap–discard
Overlap–discard and Overlap–scrap are less commonly used labels for the same method described here. However, these labels are actually better (than overlap–save) to distinguish from overlap–add, because both methods "save", but only one discards. "Save" merely refers to the fact that M − 1 input (or output) samples from segment k are needed to process segment k + 1.Extending overlap–save
The overlap-save algorithm may be extended to include other common operations of a system :- additional channels can be processed more cheaply than the first by reusing the forward FFT
- sampling rates can be changed by using different sized forward and inverse FFTs
- frequency translation (mixing) can be accomplished by rearranging frequency bins

