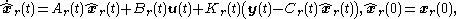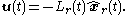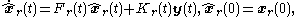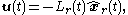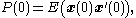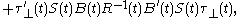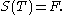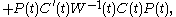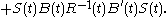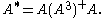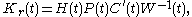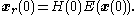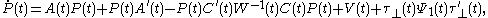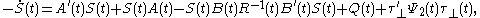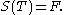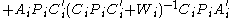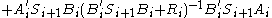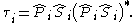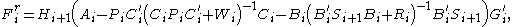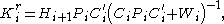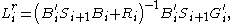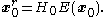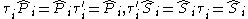Optimal projection equations
Encyclopedia
In control
, the Linear-Quadratic-Gaussian (LQG) control problem
is one of the most fundamental optimal control
problems. It concerns uncertain linear system
s disturbed by additive white Gaussian noise
, incomplete state information (i.e. not all the state variables are measured and available for feedback) also disturbed by additive white Gaussian noise and quadratic costs. Moreover the solution is unique and constitutes a linear dynamic feedback control law that is easily computed and implemented. Finally the LQG controller is also fundamental to the optimal perturbation control of non-linear systems .
The LQG controller itself is a dynamic system like the system it controls. Both systems have the same state dimension. Therefore implementing the LQG controller may be problematic if the dimension of the system state is large. The reduced-order LQG problem (fixed-order LQG problem) overcomes this by fixing a-priori the number of states of the LQG controller. This problem is more difficult to solve because it is no longer separable. Also the solution is no longer unique. Despite these facts numerical algorithms are available to solve the associated optimal projection equations which constitute necessary and sufficient conditions for a locally optimal reduced-order LQG controller .
. Let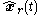 represent the state of the reduced-order LQG controller. Then the only difference is that the state dimension
represent the state of the reduced-order LQG controller. Then the only difference is that the state dimension 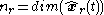 of the LQG controller is a-priori fixed to be smaller than
of the LQG controller is a-priori fixed to be smaller than  , the state dimension of the controlled system.
, the state dimension of the controlled system.
The reduced-order LQG controller is represented by the following equations,
These equations are delibarately stated in a format that equals that of the conventional full-order LQG controller
. For the reduced-order LQG control problem it is convenient to rewrite them:
where,
The matrices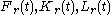 and
and  of the reduced-order LQG controller are determined by the so called optimal projection equations (OPE).
of the reduced-order LQG controller are determined by the so called optimal projection equations (OPE).
The square optimal projection matrix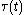 with dimension
with dimension  is central to the OPE. The rank of this matrix is almost everywhere equal to
is central to the OPE. The rank of this matrix is almost everywhere equal to 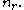 The associated projection is an oblique projection:
The associated projection is an oblique projection: 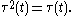 The OPE constitute four matrix differential equations. The first two equations listed below are generalizations of the matrix Riccati differential equations associated to the conventional full-order LQG controller
The OPE constitute four matrix differential equations. The first two equations listed below are generalizations of the matrix Riccati differential equations associated to the conventional full-order LQG controller
. In these equations denotes
denotes 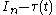 where
where  is the identity matrix of dimension
is the identity matrix of dimension  .
.
Control theory
Control theory is an interdisciplinary branch of engineering and mathematics that deals with the behavior of dynamical systems. The desired output of a system is called the reference...
, the Linear-Quadratic-Gaussian (LQG) control problem
Linear-quadratic-Gaussian control
In control theory, the linear-quadratic-Gaussian control problem is one of the most fundamental optimal control problems. It concerns uncertain linear systems disturbed by additive white Gaussian noise, having incomplete state information and undergoing control subject to quadratic costs...
is one of the most fundamental optimal control
Optimal control
Optimal control theory, an extension of the calculus of variations, is a mathematical optimization method for deriving control policies. The method is largely due to the work of Lev Pontryagin and his collaborators in the Soviet Union and Richard Bellman in the United States.-General method:Optimal...
problems. It concerns uncertain linear system
Linear system
A linear system is a mathematical model of a system based on the use of a linear operator.Linear systems typically exhibit features and properties that are much simpler than the general, nonlinear case....
s disturbed by additive white Gaussian noise
Additive white Gaussian noise
Additive white Gaussian noise is a channel model in which the only impairment to communication is a linear addition of wideband or white noise with a constant spectral density and a Gaussian distribution of amplitude. The model does not account for fading, frequency selectivity, interference,...
, incomplete state information (i.e. not all the state variables are measured and available for feedback) also disturbed by additive white Gaussian noise and quadratic costs. Moreover the solution is unique and constitutes a linear dynamic feedback control law that is easily computed and implemented. Finally the LQG controller is also fundamental to the optimal perturbation control of non-linear systems .
The LQG controller itself is a dynamic system like the system it controls. Both systems have the same state dimension. Therefore implementing the LQG controller may be problematic if the dimension of the system state is large. The reduced-order LQG problem (fixed-order LQG problem) overcomes this by fixing a-priori the number of states of the LQG controller. This problem is more difficult to solve because it is no longer separable. Also the solution is no longer unique. Despite these facts numerical algorithms are available to solve the associated optimal projection equations which constitute necessary and sufficient conditions for a locally optimal reduced-order LQG controller .
Continuous-time
The Reduced-order LQG control problem is almost identical to the conventional full-order LQG control problemLinear-quadratic-Gaussian control
In control theory, the linear-quadratic-Gaussian control problem is one of the most fundamental optimal control problems. It concerns uncertain linear systems disturbed by additive white Gaussian noise, having incomplete state information and undergoing control subject to quadratic costs...
. Let
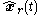 represent the state of the reduced-order LQG controller. Then the only difference is that the state dimension
represent the state of the reduced-order LQG controller. Then the only difference is that the state dimension 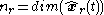 of the LQG controller is a-priori fixed to be smaller than
of the LQG controller is a-priori fixed to be smaller than  , the state dimension of the controlled system.
, the state dimension of the controlled system.The reduced-order LQG controller is represented by the following equations,
These equations are delibarately stated in a format that equals that of the conventional full-order LQG controller
Linear-quadratic-Gaussian control
In control theory, the linear-quadratic-Gaussian control problem is one of the most fundamental optimal control problems. It concerns uncertain linear systems disturbed by additive white Gaussian noise, having incomplete state information and undergoing control subject to quadratic costs...
. For the reduced-order LQG control problem it is convenient to rewrite them:
where,
-
 .
.
The matrices
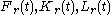 and
and  of the reduced-order LQG controller are determined by the so called optimal projection equations (OPE).
of the reduced-order LQG controller are determined by the so called optimal projection equations (OPE).The square optimal projection matrix
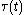 with dimension
with dimension  is central to the OPE. The rank of this matrix is almost everywhere equal to
is central to the OPE. The rank of this matrix is almost everywhere equal to 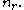 The associated projection is an oblique projection:
The associated projection is an oblique projection: 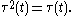 The OPE constitute four matrix differential equations. The first two equations listed below are generalizations of the matrix Riccati differential equations associated to the conventional full-order LQG controller
The OPE constitute four matrix differential equations. The first two equations listed below are generalizations of the matrix Riccati differential equations associated to the conventional full-order LQG controllerLinear-quadratic-Gaussian control
In control theory, the linear-quadratic-Gaussian control problem is one of the most fundamental optimal control problems. It concerns uncertain linear systems disturbed by additive white Gaussian noise, having incomplete state information and undergoing control subject to quadratic costs...
. In these equations
 denotes
denotes 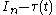 where
where  is the identity matrix of dimension
is the identity matrix of dimension  .
.-
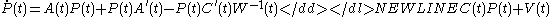
-
-
-
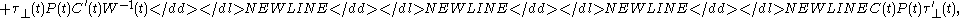
If the dimension of the LQG controller is not reduced, that is if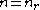 , then
, then 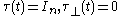 and the two equations above become the uncoupled matrix Riccati differential equations associated to the conventional full-order LQG controllerLinear-quadratic-Gaussian controlIn control theory, the linear-quadratic-Gaussian control problem is one of the most fundamental optimal control problems. It concerns uncertain linear systems disturbed by additive white Gaussian noise, having incomplete state information and undergoing control subject to quadratic costs...
and the two equations above become the uncoupled matrix Riccati differential equations associated to the conventional full-order LQG controllerLinear-quadratic-Gaussian controlIn control theory, the linear-quadratic-Gaussian control problem is one of the most fundamental optimal control problems. It concerns uncertain linear systems disturbed by additive white Gaussian noise, having incomplete state information and undergoing control subject to quadratic costs...
. If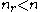 the two equations are coupled by the oblique projection
the two equations are coupled by the oblique projection 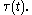 This reveals why the reduced-order LQG problem is not separable. The oblique projection
This reveals why the reduced-order LQG problem is not separable. The oblique projection 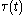 is determined from two additional matrix differential equations which involve rank conditions. Together with the previous two matrix differential equations these are the OPE. To state the additional two matrix differential equations it is convenient to introduce the following two matrices,
is determined from two additional matrix differential equations which involve rank conditions. Together with the previous two matrix differential equations these are the OPE. To state the additional two matrix differential equations it is convenient to introduce the following two matrices,
-
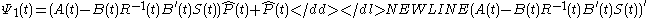
-

Then the two additional matrix differential equations that complete the OPE read as follows,
-
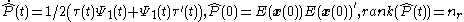 almost everywhere,
almost everywhere,
-
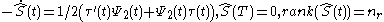 almost everywhere,
almost everywhere,
with,
Here * denotes the group generalized inverse or Drazin inverseDrazin inverseIn mathematics, the Drazin inverse, named after Michael P. Drazin, is a kind of generalized inverse of a matrix.Let A be a square matrix. The index of A is the least nonnegative integer k such that rank = rank...
that is unique and given by,
where + denotes the Moore-Penrose pseudoinverse.
The matrices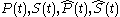 must all be nonnegative symmetric. Then they constitute a solution of the OPE that determines the reduced-order LQG controller matrices
must all be nonnegative symmetric. Then they constitute a solution of the OPE that determines the reduced-order LQG controller matrices 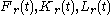 and
and  :
:
-
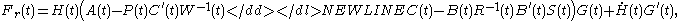
In the equations above the matrices are two matrices with the following properties,
are two matrices with the following properties,
-
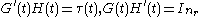 almost everywhere.
almost everywhere.
They can be obtained from a projective factorization of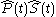 .
.
The OPE can be stated in many different ways that are all equivalent. To identify the equivalent representations the following identities are especially useful,
Using these identities one may for instance rewrite the first two of the optimal projection equations as follows,
This representation is both relatively simple and suitable for numerical computations.
If all the matrices in the reduced-order LQG problem formulation are time-invariant and if the horizon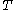 tends to infinity, the optimal reduced-order LQG controller becomes time-invariant and so do the OPE . In that case the derivatives on the left hand side of the OPE are zero.
tends to infinity, the optimal reduced-order LQG controller becomes time-invariant and so do the OPE . In that case the derivatives on the left hand side of the OPE are zero.
Discrete-time
Similar to the continuous-time case in the discrete-time case the difference with the conventional discrete-time full-order LQG problemLinear-quadratic-Gaussian controlIn control theory, the linear-quadratic-Gaussian control problem is one of the most fundamental optimal control problems. It concerns uncertain linear systems disturbed by additive white Gaussian noise, having incomplete state information and undergoing control subject to quadratic costs...
is the a-priori fixed reduced-order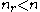 of the LQG controller state dimension. As in continuous-time to state the discrete-time OPE it is convenient to introduce the following two matrices,
of the LQG controller state dimension. As in continuous-time to state the discrete-time OPE it is convenient to introduce the following two matrices,
-
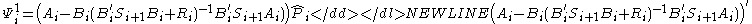
-
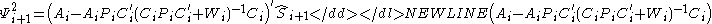
Then the discrete-time OPE read as follows,
-
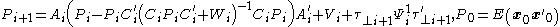 .
. -
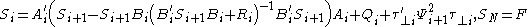 .
. almost everywhere,
almost everywhere, almost everywhere.
almost everywhere.
The oblique projection matrix is given by,
The nonnegative symmetric matrices that solve the discrete-time OPE determine the reduced-order LQG controller matrices
that solve the discrete-time OPE determine the reduced-order LQG controller matrices  and
and 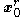 :
:
In the equations above the matrices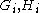 are two matrices with the following properties,
are two matrices with the following properties,
-
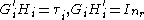 almost everywhere.
almost everywhere.
They can be obtained from a projective factorization of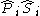 . To identify equivalent representations of the discrete-time OPE the following identities are especially useful,
. To identify equivalent representations of the discrete-time OPE the following identities are especially useful,
As in the continuous-time case if all the matrices in the problem formulation are time-invariant and if the horizon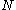 tends to infinity the reduced-order LQG controller becomes time-invariant. Then the discrete-time OPE converge to a steady state solution that determines the time-invariant reduced-order LQG controller.
tends to infinity the reduced-order LQG controller becomes time-invariant. Then the discrete-time OPE converge to a steady state solution that determines the time-invariant reduced-order LQG controller.
The discrete-time OPE apply also to discrete-time systems with variable state, input and output dimensions (discrete-time systems with time-varying dimensions). Such systems arise in the case of digital controller design if the sampling occurs asynchronously. -
-
-
-
-
-
-
-
-