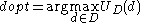Optimal decision
Encyclopedia
An optimal decision is a decision such that no other available decision options will lead to a better outcome. It is an important concept in decision theory
. In order to compare the different decision outcomes, one commonly assigns a relative utility to each of them. If there is uncertainty in what the outcome will be, the optimal decision maximizes the expected (average) utility.
Sometimes, the equivalent problem of minimizing loss
is considered, particularly in financial situations, where the utility is defined as economic gain.
"Utility" is only an arbitrary term for quantifying the desirability of a particular decision outcome and not necessarily related to "usefulness." For example, it may well be the optimal decision for someone to buy a sports car rather than a station wagon, if the outcome in terms of another criterion (e.g., effect on personal image) is more desirable, even given the higher cost and lack of versatility of the sports car.
In case the decision outcome is subject to uncertainty, an optimal decision is maximizing the expected utility
.
The problem of finding the optimal decision is a mathematical optimization problem. In practice, few people verify that their decisions are optimal, but instead use more intuitive approaches to make decisions that are "good enough."
A more formal approach may be used when the decision is important enough to motivate the time it takes to analyze it, or when it is too complex to solve with more simple intuitive approaches, such as with a large number of available decision options and a complex decision – outcome relationship.
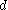 in a set
in a set 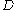 of available decision options will lead to an outcome
of available decision options will lead to an outcome 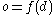 . All possible outcomes form the set
. All possible outcomes form the set 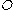 .
.
Assigning a utility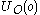 to every outcome, we can define the utility of a particular decision
to every outcome, we can define the utility of a particular decision  as
as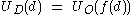
We can then define an optimal decision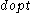 as one that maximizes
as one that maximizes  :
: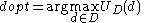
Solving the problem can thus be divided into three steps:
given a decision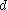 , we know the probability distribution for the possible outcomes described by the conditional probability density
, we know the probability distribution for the possible outcomes described by the conditional probability density 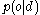 . We can then calculate the expected utility of decision
. We can then calculate the expected utility of decision  as
as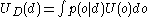 ,
,
where the integral is taken over the whole set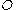 (DeGroot, pp 121)
(DeGroot, pp 121)
An optimal decision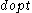 is then one that maximizes
is then one that maximizes  , just as above
, just as above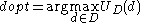
Decision theory
Decision theory in economics, psychology, philosophy, mathematics, and statistics is concerned with identifying the values, uncertainties and other issues relevant in a given decision, its rationality, and the resulting optimal decision...
. In order to compare the different decision outcomes, one commonly assigns a relative utility to each of them. If there is uncertainty in what the outcome will be, the optimal decision maximizes the expected (average) utility.
Sometimes, the equivalent problem of minimizing loss
Loss function
In statistics and decision theory a loss function is a function that maps an event onto a real number intuitively representing some "cost" associated with the event. Typically it is used for parameter estimation, and the event in question is some function of the difference between estimated and...
is considered, particularly in financial situations, where the utility is defined as economic gain.
"Utility" is only an arbitrary term for quantifying the desirability of a particular decision outcome and not necessarily related to "usefulness." For example, it may well be the optimal decision for someone to buy a sports car rather than a station wagon, if the outcome in terms of another criterion (e.g., effect on personal image) is more desirable, even given the higher cost and lack of versatility of the sports car.
In case the decision outcome is subject to uncertainty, an optimal decision is maximizing the expected utility
Expected utility hypothesis
In economics, game theory, and decision theory the expected utility hypothesis is a theory of utility in which "betting preferences" of people with regard to uncertain outcomes are represented by a function of the payouts , the probabilities of occurrence, risk aversion, and the different utility...
.
The problem of finding the optimal decision is a mathematical optimization problem. In practice, few people verify that their decisions are optimal, but instead use more intuitive approaches to make decisions that are "good enough."
A more formal approach may be used when the decision is important enough to motivate the time it takes to analyze it, or when it is too complex to solve with more simple intuitive approaches, such as with a large number of available decision options and a complex decision – outcome relationship.
Formal mathematical description
Each decision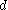 in a set
in a set 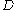 of available decision options will lead to an outcome
of available decision options will lead to an outcome 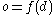 . All possible outcomes form the set
. All possible outcomes form the set 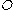 .
.Assigning a utility
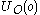 to every outcome, we can define the utility of a particular decision
to every outcome, we can define the utility of a particular decision  as
as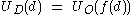
We can then define an optimal decision
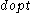 as one that maximizes
as one that maximizes  :
: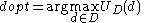
Solving the problem can thus be divided into three steps:
- predicting the outcome
 for every decision
for every decision 
- assigning a utility
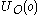 to every outcome
to every outcome 
- finding the decision
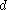 that maximizes
that maximizes 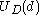
Under uncertainty in outcome
In case it is not possible to predict with certainty what will be the outcome of a particular decision, a probabilistic approach is necessary. In its most general form, it can be expressed as follows:given a decision
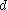 , we know the probability distribution for the possible outcomes described by the conditional probability density
, we know the probability distribution for the possible outcomes described by the conditional probability density 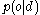 . We can then calculate the expected utility of decision
. We can then calculate the expected utility of decision  as
as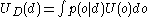 ,
,where the integral is taken over the whole set
 (DeGroot, pp 121)
(DeGroot, pp 121)An optimal decision
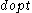 is then one that maximizes
is then one that maximizes  , just as above
, just as above