
One-in-three 3SAT
Encyclopedia
In computational complexity theory
, one-in-three 3SAT (also known variously as 1-in-3 SAT and exactly-1 3SAT) is an NP-complete
problem. The problem is a variant of the 3-satisfiability problem
(3SAT). Like 3SAT, the input instance is a collection of clauses, where each clause consists of exactly three literals, and each literal is either a variable or its negation. The one-in-three 3SAT problem is to determine whether there exists a truth assignment to the variables so that each clause has exactly one true literal (and thus exactly two false literals). (In contrast, ordinary 3SAT requires that every clause has at least one true literal.)
One-in-three 3SAT is listed as NP-complete
problem LO4 in the standard reference, Computers and Intractability: A Guide to the Theory of NP-Completeness
by Michael R. Garey and David S. Johnson
. It was proved to be NP-complete by Thomas J. Schaefer as a special case of Schaefer's dichotomy theorem, which asserts that any problem generalizing Boolean satisfiability in a certain way is either in the class P or is NP-complete.
Schaefer gives a construction allowing an easy polynomial-time reduction
from 3SAT to one-in-three 3SAT. Let "(x or y or z)" be a clause in a 3CNF formula. Add six new boolean variables a, b, c, d, e, and f, to be used to simulate this clause and no other. Let R(u,v,w) be a predicate that is true if and only if exactly one of the booleans u, v, and w
is true. Then the formula "R(x,a,d) and R(y,b,d) and R(a,b,e) and R(c,d,f) and R(z,c,false)" is satisfiable by some setting of the new variables if and only if at least one of x, y,
or z is true. We may thus convert any 3SAT instance with m clauses and n variables into a one-in-three 3SAT instance with 5m clauses and n + 6m variables.
Another reduction involves only four new variables and three clauses: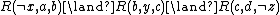 .
.
The one-in-three 3SAT problem is often used in the literature as a known NP-complete problem in a reduction to show that other problems are NP-complete.
We can think of the instance to one-in-three SAT as a graph
, with a vertex for each variable and each clause, and an edge connecting a variable to a clause if it occurs (positively or negatively) in that clause. In planar one-in-three 3SAT, this graph is assumed to be planar
. This problem is also NP-complete.
Computational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
, one-in-three 3SAT (also known variously as 1-in-3 SAT and exactly-1 3SAT) is an NP-complete
NP-complete
In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...
problem. The problem is a variant of the 3-satisfiability problem
3sat
3sat is the name of a public, advertising-free, television network in Central Europe. The programming is in German and is broadcast primarily within Germany, Austria and Switzerland .3sat was established for cultural...
(3SAT). Like 3SAT, the input instance is a collection of clauses, where each clause consists of exactly three literals, and each literal is either a variable or its negation. The one-in-three 3SAT problem is to determine whether there exists a truth assignment to the variables so that each clause has exactly one true literal (and thus exactly two false literals). (In contrast, ordinary 3SAT requires that every clause has at least one true literal.)
One-in-three 3SAT is listed as NP-complete
NP-complete
In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...
problem LO4 in the standard reference, Computers and Intractability: A Guide to the Theory of NP-Completeness
by Michael R. Garey and David S. Johnson
David S. Johnson
David Stifler Johnson is a computer scientist specializing in algorithms and optimization. He is currently the head of the Algorithms and Optimization Department of AT&T Labs Research. He was awarded the 2010 Knuth Prize....
. It was proved to be NP-complete by Thomas J. Schaefer as a special case of Schaefer's dichotomy theorem, which asserts that any problem generalizing Boolean satisfiability in a certain way is either in the class P or is NP-complete.
Schaefer gives a construction allowing an easy polynomial-time reduction
Polynomial-time reduction
In computational complexity theory a polynomial-time reduction is a reduction which is computable by a deterministic Turing machine in polynomial time. If it is a many-one reduction, it is called a polynomial-time many-one reduction, polynomial transformation, or Karp reduction...
from 3SAT to one-in-three 3SAT. Let "(x or y or z)" be a clause in a 3CNF formula. Add six new boolean variables a, b, c, d, e, and f, to be used to simulate this clause and no other. Let R(u,v,w) be a predicate that is true if and only if exactly one of the booleans u, v, and w
is true. Then the formula "R(x,a,d) and R(y,b,d) and R(a,b,e) and R(c,d,f) and R(z,c,false)" is satisfiable by some setting of the new variables if and only if at least one of x, y,
or z is true. We may thus convert any 3SAT instance with m clauses and n variables into a one-in-three 3SAT instance with 5m clauses and n + 6m variables.
Another reduction involves only four new variables and three clauses:
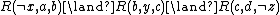 .
.The one-in-three 3SAT problem is often used in the literature as a known NP-complete problem in a reduction to show that other problems are NP-complete.
Variations
In monotone one-in-three 3SAT, every literal is simply a variable; in other words, there is no negation. This problem is also NP-complete, as proved by Schaefer. Indeed, this was the original problem from Schaefer's point of view, which he called ONE-IN-THREE SATISFIABILITY.We can think of the instance to one-in-three SAT as a graph
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
, with a vertex for each variable and each clause, and an edge connecting a variable to a clause if it occurs (positively or negatively) in that clause. In planar one-in-three 3SAT, this graph is assumed to be planar
Planar graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
. This problem is also NP-complete.

