
Numerical 3-dimensional matching
Encyclopedia
Numerical 3-dimensional matching is a strongly NP-complete decision problem. It is given by three multisets of integers  ,
,  and
and  , each containing
, each containing  elements, and a bound
elements, and a bound 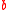 . The goal is to select a subset
. The goal is to select a subset 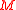 of
of 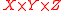 such that every integer in
such that every integer in  ,
,  and
and  occurs exactly once and that for every triple
occurs exactly once and that for every triple 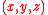 in the subset
in the subset  holds.
holds.
This problem is labeled as [SP16] in .
 ,
, 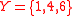 and
and 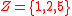 , and
, and 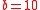 . This instance has a solution, namely
. This instance has a solution, namely 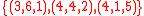 . Note that each triple sums to
. Note that each triple sums to 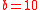 . The set
. The set 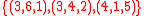 is not a solution for several reasons: not every number is used (a
is not a solution for several reasons: not every number is used (a 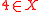 is missing), a number is used too often (the
is missing), a number is used too often (the  ) and not every triple sums to
) and not every triple sums to 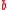 (since
(since  ). However, there is at least one solution to this problem, which is the property we are interested in with decision problems.
). However, there is at least one solution to this problem, which is the property we are interested in with decision problems.
If we would take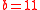 for the same
for the same  ,
,  and
and  , this problem would have no solution (all numbers sum to
, this problem would have no solution (all numbers sum to  , which is not equal to
, which is not equal to  in this case).
in this case).
To prove NP-completeness of the numerical 3-dimensional matching, the proof is similar, but a reduction from 3-dimensional matching via the numerical 4-dimensional matching problem should be used.
 ,
,  and
and  , each containing
, each containing  elements, and a bound
elements, and a bound 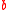 . The goal is to select a subset
. The goal is to select a subset 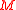 of
of 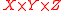 such that every integer in
such that every integer in  ,
,  and
and  occurs exactly once and that for every triple
occurs exactly once and that for every triple 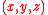 in the subset
in the subset  holds.
holds.This problem is labeled as [SP16] in .
Example
Take ,
, 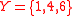 and
and 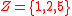 , and
, and 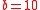 . This instance has a solution, namely
. This instance has a solution, namely 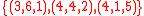 . Note that each triple sums to
. Note that each triple sums to 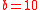 . The set
. The set 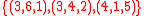 is not a solution for several reasons: not every number is used (a
is not a solution for several reasons: not every number is used (a 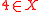 is missing), a number is used too often (the
is missing), a number is used too often (the  ) and not every triple sums to
) and not every triple sums to 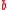 (since
(since  ). However, there is at least one solution to this problem, which is the property we are interested in with decision problems.
). However, there is at least one solution to this problem, which is the property we are interested in with decision problems.If we would take
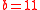 for the same
for the same  ,
,  and
and  , this problem would have no solution (all numbers sum to
, this problem would have no solution (all numbers sum to  , which is not equal to
, which is not equal to  in this case).
in this case).Related problems
Every instance of the Numerical 3-dimensional matching problem is an instance of both the 3-partition problem, and the 3-dimensional matching problem.Proof of NP-completeness
NP-completeness of the 3-partition problem is stated by Garey and Johnson in "Computers and Intractability; A Guide to the Theory of NP-Completeness". It is done by a reduction from 3-dimensional matching via 4-partition.To prove NP-completeness of the numerical 3-dimensional matching, the proof is similar, but a reduction from 3-dimensional matching via the numerical 4-dimensional matching problem should be used.

