Nullcline
Encyclopedia
Nullclines, sometimes called zero-growth isoclines, are encountered in a system of ordinary differential equation
s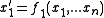
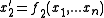
where the
here represents a derivative with respect to another parameter, such as time 
. Nullclines are the geometric shape for which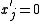 
for any 
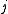. The fixed point
s of the system are located where all of the nullclines intersect.
In a two-dimensional linear system, the nullclines can be represented by two lines on a two-dimensional plot.
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
s
-
- .
- .
- .
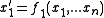
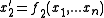
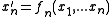
where the
here represents a derivative with respect to another parameter, such as time . Nullclines are the geometric shape for which 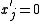for any 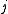. The fixed pointFixed point (mathematics)
In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
s of the system are located where all of the nullclines intersect.
In a two-dimensional linear system, the nullclines can be represented by two lines on a two-dimensional plot.
External links
- Notes from MIT OpenCourseWareMIT OpenCourseWareMIT OpenCourseWare is an initiative of the Massachusetts Institute of Technology to put all of the educational materials from its undergraduate- and graduate-level courses online, partly free and openly available to anyone, anywhere. MIT OpenCourseWare is a large-scale, web-based publication of...
- SOS Mathematics: Qualitative Analysis