Novikov's condition
Encyclopedia
In probability theory, Novikov's condition is the sufficient condition for a stochastic process which takes the form of the Radon-Nikodym derivative in Girsanov's theorem to be a martingale. If satisfied together with other conditions, Girsanov's theorem may be applied to a Brownian Motion stochastic process
to change from the original measure to the new measure defined by the Radon-Nikodym derivative.
This condition was suggested and proved by Professor Alexander Novikov
. There are other results which may be used to show that the Radon-Nikodym derivative is a martingale, such as the more general criterion Kazamaki's condition
, however Novikov Condition is the most well-known result.
Assume that
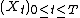is a real valued adapted process on the probability space 
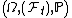and 
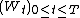is an adapted Brownian motion
:
If the condition
Stochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
to change from the original measure to the new measure defined by the Radon-Nikodym derivative.
This condition was suggested and proved by Professor Alexander Novikov
Alexander Novikov (professor)
Alexander Novikov is a professor of Mathematics at the Department of Mathematical Sciences, University of Technology Sydney.Prior to this current appointment in 1999 he was Leading Research Fellow at the Steklov Mathematical Institute and Senior Lecture at the University of Newcastle .Alexander...
. There are other results which may be used to show that the Radon-Nikodym derivative is a martingale, such as the more general criterion Kazamaki's condition
Kazamaki's condition
Kazamaki's condition gives a sufficient criterion ensuring that the Doléans-Dade exponential of a local martingale is a true martingale. In mathematics, this is particularly important if one wishes to apply Girsanov's theorem in order to perform a change of measure...
, however Novikov Condition is the most well-known result.
Assume that
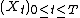is a real valued adapted process on the probability space 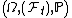and 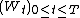is an adapted Brownian motionBrownian motion
Brownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...
:
If the condition
-
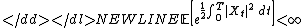
is fulfilled then the process
-
is a martingale under the probability measure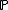
and the filtration 
.
-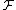