Notation for theoretic scheduling problems
Encyclopedia
A convenient notation for theoretic scheduling problems was introduced by Ronald Graham
, Eugene Lawler
, Jan Karel Lenstra
and Alexander Rinnooy Kan
. It consists of three fields: α
, β
and γ
.
Each field may be a comma separated list of words. The α field describes the machine environment, β the job characteristics, and γ the objective function.
1
P
Q
R
The last two letters might be followed by a the number of machines which is then fixed, here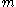
stands then for a fixed number.
F : flow shop problem
J : job shop problem
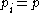, or 
) or 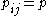even of unit length (
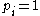, or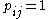 
). This makes a difference because all release times, deadlines are assumed to be integer.
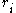
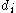
pmtn
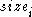
Precedence relations might be given for the jobs, in form of a partial order, meaning that if i is a predecessor of i' in that order, i' can start only when i is completed.
prec
sp-tree, tree, intree, outtree, chain
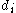and the completion time 
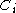of job 
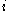. We define lateness 
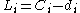, earliness 
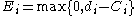, tardiness 
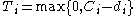, unit penalty 
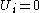if 
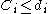and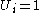 
otherwise. The common objective functions are 
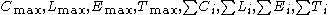or weighted version of these sums, where every job comes with a priority 
.
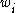Ronald Graham
Ronald Lewis Graham is a mathematician credited by the American Mathematical Society as being "one of the principal architects of the rapid development worldwide of discrete mathematics in recent years"...
, Eugene Lawler
Eugene Lawler
Eugene Leighton Lawler was an American computer scientist, a professor of computer science at the University of California, Berkeley.-Academic life:...
, Jan Karel Lenstra
Jan Karel Lenstra
Jan Karel Lenstra is a Dutch mathematician and operations researcher, known for his work on scheduling algorithms, local search, and the travelling salesman problem....
and Alexander Rinnooy Kan
Alexander Rinnooy Kan
Alexander Hendrik George Rinnooy Kan is a Dutch mathematician and business leader. The Dutch newspaper de Volkskrant named him the most influential man in the Netherlands in 2007, 2008 and 2009....
. It consists of three fields: α
Alpha (letter)
Alpha is the first letter of the Greek alphabet. In the system of Greek numerals it has a value of 1. It was derived from the Phoenician letter Aleph...
, β
Beta (letter)
Beta is the second letter of the Greek alphabet. In Ancient Greek, beta represented the voiced bilabial plosive . In Modern Greek, it represents the voiced labiodental fricative ....
and γ
Gamma
Gamma is the third letter of the Greek alphabet. In the system of Greek numerals it has a value of 3. It was derived from the Phoenician letter Gimel . Letters that arose from Gamma include the Roman C and G and the Cyrillic letters Ge Г and Ghe Ґ.-Greek:In Ancient Greek, gamma represented a...
.
Each field may be a comma separated list of words. The α field describes the machine environment, β the job characteristics, and γ the objective function.
Single stage problems
Each job comes with a given processing time.1
- there is a single machine
P
- there are
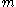parallel identical machines
Q
- there are
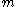parallel machines with different given speeds, length of job 
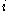on machine 
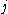is the processing time 
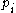divided by speed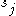 
R
- there are
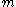parallel unrelated machines, there are given processing times 
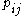for job 
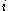on machine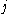 
The last two letters might be followed by a the number of machines which is then fixed, here
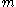stands then for a fixed number.Multi-stage problem
O : open shop problemOpen Shop Scheduling
The open shop scheduling problem is a scheduling problem where, given n jobs and m workstations, each job has to visit a workstation at least once. The order in which this happens is not relevant .- NP-hardness :The OSSP can be solved in polynomial time for two machines...
F : flow shop problem
Flow Shop Scheduling Problem
Flow Shop Scheduling Problems, or FSPs, are a class of scheduling problems with a work shop or group shop in which the flow control shall enable an appropriate sequencing for each job and for processing on a set of machines or with other resources 1,2,...,m in compliance with given processing orders...
J : job shop problem
Job Shop Scheduling
Job shop scheduling is an optimization problem in computer science in which ideal jobs are assigned to resources at particular times. The most basic version is as follows:...
Job characteristics
The processing time may be equal for all jobs (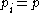, or 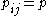) or even of unit length (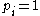, or 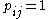). This makes a difference because all release times, deadlines are assumed to be integer.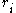
- for each job a release time is given before which it cannot be scheduled, default is 0.
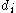
- for each job a deadline is given after which it cannot be scheduled. If the objective is
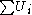for example, then this field is implicitly assumed.
pmtn
- the jobs may be preempted and execution resumed later, possibly on a different machine
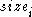
- Each job comes with a number of machines on which it must be scheduled at the same time, default is 1.
Precedence relations might be given for the jobs, in form of a partial order, meaning that if i is a predecessor of i' in that order, i' can start only when i is completed.
prec
- an arbitrary precedence relation is given
sp-tree, tree, intree, outtree, chain
- specific partial orders
Objective functions
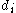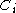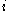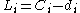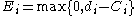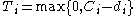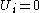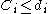Most objective functions depend on the deadline and the completion time of job . We define lateness , earliness , tardiness , unit penalty if and 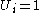otherwise. The common objective functions are 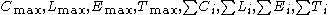or weighted version of these sums, where every job comes with a priority .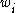