Nonnegative rank (linear algebra)
Encyclopedia
In linear algebra
, the nonnegative rank of a nonnegative matrix
is a concept similar to the usual linear rank
of a real matrix, but adding the requirement that certain coefficients and entries of vectors/matrices have to be nonnegative.
For example, the linear rank
of a matrix is the smallest number of vectors, such that every column of the matrix can be written as a linear combination of those vectors. For the nonnegative rank, it is required that the vectors must have nonnegative entries, and also that the coefficients in the linear combinations are nonnegative.
slightly. Apart from the definition give above, there is the following: The nonnegative rank of a nonnegative m×n-matrix A is equal to the smallest number q such there exists a nonnegative m×q-matrix B and a nonnegative q×n-matrix C such that A = BC (the usual matrix product). To obtain the linear rank, drop the condition that B and C must be nonnegative.
Further, the nonnegative rank it the smallest number of nonnegative rank-one matrices into which the matrix can be decomposed additively:
In the case rank(A) ≥ 3, however, rank(A) < rank+(A) is possible. For example, the matrix
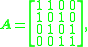
satisfies rank(A) = 3 < 4 = rank+(A) [2].
It has been proved that determining whether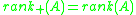
is NP-hard.
Obvious questions concerning the complexity of nonnegative rank computation remain unanswered to date. For example, the complexity of determining the nonnegative rank of matrices of fixed rank k is unknown for k > 2.
: The minimum number of facets
of an extension of a polyhedron
P is equal to the nonnegative rank of its so-called slack matrix.
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, the nonnegative rank of a nonnegative matrix
Nonnegative matrix
A nonnegative matrix is a matrix in which all the elements are equal to or greater than zeroA positive matrix is a matrix in which all the elements are greater than zero...
is a concept similar to the usual linear rank
Rank (linear algebra)
The column rank of a matrix A is the maximum number of linearly independent column vectors of A. The row rank of a matrix A is the maximum number of linearly independent row vectors of A...
of a real matrix, but adding the requirement that certain coefficients and entries of vectors/matrices have to be nonnegative.
For example, the linear rank
Rank (linear algebra)
The column rank of a matrix A is the maximum number of linearly independent column vectors of A. The row rank of a matrix A is the maximum number of linearly independent row vectors of A...
of a matrix is the smallest number of vectors, such that every column of the matrix can be written as a linear combination of those vectors. For the nonnegative rank, it is required that the vectors must have nonnegative entries, and also that the coefficients in the linear combinations are nonnegative.
Formal Definition
There are several equivalent definitions, all modifying the definition of the linear rankRank (linear algebra)
The column rank of a matrix A is the maximum number of linearly independent column vectors of A. The row rank of a matrix A is the maximum number of linearly independent row vectors of A...
slightly. Apart from the definition give above, there is the following: The nonnegative rank of a nonnegative m×n-matrix A is equal to the smallest number q such there exists a nonnegative m×q-matrix B and a nonnegative q×n-matrix C such that A = BC (the usual matrix product). To obtain the linear rank, drop the condition that B and C must be nonnegative.
Further, the nonnegative rank it the smallest number of nonnegative rank-one matrices into which the matrix can be decomposed additively:
where Rj ≥ 0 stands for "Rj is nonnegative". (To obtain the usual linear rank, drop the condition that the Rj have to be nonnegative.)
Given a nonnegative 
matrix A the nonnegative rank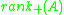 
of A satisfies
where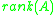 
denotes the usual linear rankRank (linear algebra)The column rank of a matrix A is the maximum number of linearly independent column vectors of A. The row rank of a matrix A is the maximum number of linearly independent row vectors of A...
of A.
A Fallacy
The rank of the matrix A is the largest number of columns which are linearly independent, i.e., none of the selected columns can be written as a linear combination of the other selected columns. It is not true that adding nonnegativity to this characterization gives the nonnegative rank: The nonnegative rank is in general strictly greater than the largest number of columns such that no selected column can be written as a nonnegative linear combination of the other selected columns.Connection with the linear rank
It is always true that rank(A) ≤ rank+(A). In fact rank+(A) = rank(A) holds whenever rank(A) ≤ 2 [2].In the case rank(A) ≥ 3, however, rank(A) < rank+(A) is possible. For example, the matrix
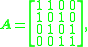
satisfies rank(A) = 3 < 4 = rank+(A) [2].
Computing the nonnegative rank
The nonnegative rank of a matrix can be determined algorithmically.It has been proved that determining whether
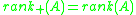is NP-hard.Obvious questions concerning the complexity of nonnegative rank computation remain unanswered to date. For example, the complexity of determining the nonnegative rank of matrices of fixed rank k is unknown for k > 2.
Ancillary Facts
Nonnegative rank has important applications in Combinatorial optimizationCombinatorial optimization
In applied mathematics and theoretical computer science, combinatorial optimization is a topic that consists of finding an optimal object from a finite set of objects. In many such problems, exhaustive search is not feasible...
: The minimum number of facets
Facets
-Personnel:*Jim Croce - guitar, vocals*Richard Croce - percussion*Mike DiBenedetto - keyboards*Karl Fehrenbach - guitar, banjo*Ken Cavender - bass-Production:*Producer: Joe Salviuolo*Arrangements: Jim Croce, Eric Von Schmidt...
of an extension of a polyhedron
Extension of a polyhedron
In mathematics, in particular in the theory of polyhedra and polytopes, an extension of a polyhedron P is a polyhedron Q together with an affine or, more generally, projective map π mapping Q onto P....
P is equal to the nonnegative rank of its so-called slack matrix.