
No-three-in-line problem
Encyclopedia
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in the area of discrete geometry
Discrete geometry
Discrete geometry and combinatorial geometry are branches of geometry that study combinatorial properties and constructive methods of discrete geometric objects. Most questions in discrete geometry involve finite or discrete sets of basic geometric objects, such as points, lines, planes, circles,...
, the no-three-in-line-problem, introduced by Henry Dudeney
Henry Dudeney
Henry Ernest Dudeney was an English author and mathematician who specialised in logic puzzles and mathematical games. He is known as one of the country's foremost creators of puzzles...
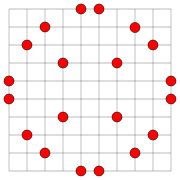
in 1917, asks for the maximum number of points that can be placed in the n × n grid so that no three points are collinear. This number is at most 2n, since if 2n + 1 points are placed in the grid some row will contain three points.
Lower bounds
Paul ErdősPaul Erdos
Paul Erdős was a Hungarian mathematician. Erdős published more papers than any other mathematician in history, working with hundreds of collaborators. He worked on problems in combinatorics, graph theory, number theory, classical analysis, approximation theory, set theory, and probability theory...
(in Roth, 1951) observed that, when n is a prime number, the set of n grid points (i, i2 mod n), for 0 ≤ i < n, contains no three collinear points. When n is not prime, one can perform this construction for a p × p grid contained in the n × n grid, where p is the largest prime that is at most n. As a consequence, for any ε and any sufficiently large n, one can placen
points in the n × n grid with no three points collinear.
Erdős' bound has been improved subsequently: Hall et al. (1975) show that, when n/2 is prime, one can obtain a solution with 3(n - 2)/2 points by placing points on the hyperbola
Hyperbola
In mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...
xy ≡ k (mod n/2) for a suitable k. Again, for arbitrary n one can perform this construction for a prime near n/2 to obtain a solution withn
points.
Conjectured upper bounds
Guy and Kelly (1968) conjectured that one cannot do better, for large n, than cn with
As recently as March, 2004, Gabor Ellmann notes an error in the original paper of Guy and Kelly's heuristic reasoning,
which if corrected, results in

Applications
The Heilbronn triangle problemHeilbronn triangle problem
In mathematics, the Heilbronn triangle problem is a typical question in the area of irregularities of distribution, within elementary geometry....
asks for the placement of n points in a unit square that maximizes the area of the smallest triangle formed by three of the points. By applying Erdős' construction of a set of grid points with no three collinear points, one can find a placement in which the smallest triangle has area

Generalizations
A noncollinear placement of n points can also be interpreted as a graph drawingGraph drawing
Graph drawing is an area of mathematics and computer science combining methods from geometric graph theory and information visualization to derive two-dimensional depictions of graphs arising from applications such as social network analysis, cartography, and bioinformatics...
of the complete graph
Complete graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
in such a way that, although edges cross, no edge passes through a vertex. Erdős' construction above can be generalized to show that every n-vertex k-colorable graph has such a drawing in a O(n) x O(k) grid (Wood 2005).
Non-collinear sets of points in the three-dimensional grid were considered by Pór and Wood (2007). They proved that the maximum number of points in the n x n x n grid with no three points collinear is
 .
.Similarly to Erdős's 2D construction, this can be accomplished by using points
(x, y, x2+y2) mod p, where p is a prime congruent to 3 mod 4.
One can also consider graph drawings in the three-dimensional grid. Here the non-collinearity condition means that a vertex should not lie on a non-adjacent edge, but it is normal to work with the stronger requirement that no two edges cross (Pach et al. 1998; Dujmović et al. 2005; Di Giacomo 2005).
Small values of n
For n ≤ 40, it is known that 2n points may be placed with no three in a line. The numbers of solutions (not counting reflections and rotations as distinct) for small n = 2, 3, ..., are- 1, 1, 4, 5, 1111 (number)11 is the natural number following 10 and preceding 12.Eleven is the first number which cannot be counted with a human's eight fingers and two thumbs additively. In English, it is the smallest positive integer requiring three syllables and the largest prime number with a single-morpheme name...
, 2222 (number)22 is the natural number following 21 and preceding 23.- In mathematics :Twenty-two is an even composite number, its proper divisors being 1, 2 and 11....
, 5757 (number)57 is the natural number following 56 and preceding 58.- In mathematics :Fifty-seven is the sixteenth discrete semiprime and the sixth in the family. With 58 it forms the fourth discrete bi-prime pair. 57 has an aliquot sum of 23 and is the first composite member of the 23-aliquot tree...
, 51, 156156 (number)156 is the number equal to 100 + 50 + 6, following 155 and followed by 157.-In mathematics:It is a pronic number, a dodecagonal number, a refactorable number and a Harshad number.156 is a repdigit in base 5 .-In the military:...
, 158158 (number)158 is an even whole number following 157 and preceding 159.-In mathematics:* 158 is a nontotient, since there is no integer with 158 coprimes below it.* 158 is a Perrin number, appearing after 68, 90, 119....
, 566, 499, 1366, ... .

