Nevanlinna–Pick interpolation
Encyclopedia
In complex analysis
, Nevanlinna–Pick interpolation is the problem of finding a holomorphic function
from the unit disc to the unit disc (denoted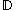
), which takes specified points to specified points. Equivalently, it is the problem of finding a holomorphic function f which interpolates a data set, subject to the upper bound 
for all 
.
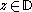More formally, if z1, ..., zN and w1, ..., wN are collections of points in the unit disc, the Nevanlinna–Pick problem is the problem of finding a holomorphic function
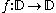
such that
The problem was independently solved by G. Pick
and R. Nevanlinna
in 1916 and 1919 respectively. It was shown that such an f exists if and only if the Pick matrix
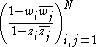
is positive semi-definite. Also, the function f is unique if and only if the Pick matrix has zero determinant
. Pick's original proof was based on Blaschke product
s.
H 2 is a reproducing kernel Hilbert space
, and that its reproducing kernel (known as the Szegő
kernel) is
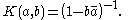
Because of this, the Pick matrix can be rewritten as
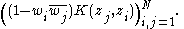
This description of the solution has motivated various attempts to generalise Nevanlinna and Pick's result.
The Nevanlinna–Pick problem can be generalised to that of finding a holomorphic function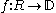
that interpolates a given set of data, where R is now an arbitrary region of the complex plane.
M. B. Abrahamse showed that if the boundary of R consists of finitely many analytic curves (say n + 1), then an interpolating function f exists if and only if
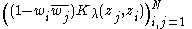
is a positive semi-definite matrix, for all λ in the n-torus. Here, the Kλs are the reproducing kernels corresponding to a particular set of reproducing kernel Hilbert spaces, which are related to the set R. It can also be shown that f is unique if and only if one of the Pick matrices has zero determinant.
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
, Nevanlinna–Pick interpolation is the problem of finding a holomorphic function
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
from the unit disc to the unit disc (denoted
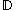), which takes specified points to specified points. Equivalently, it is the problem of finding a holomorphic function f which interpolates a data set, subject to the upper bound for all 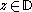.More formally, if z1, ..., zN and w1, ..., wN are collections of points in the unit disc, the Nevanlinna–Pick problem is the problem of finding a holomorphic function
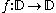
such that
- f(wi) = zi for all i between 1 and N.
The problem was independently solved by G. Pick
Georg Alexander Pick
Georg Alexander Pick was an Austrian mathematician. He was born to Josefa Schleisinger and Adolf Josef Pick. He died in the Theresienstadt concentration camp. Today he is best known for Pick's formula for determining the area of lattice polygons...
and R. Nevanlinna
Rolf Nevanlinna
Rolf Herman Nevanlinna was one of the most famous Finnish mathematicians. He was particularly appreciated for his work in complex analysis.- The Nevanlinna family :...
in 1916 and 1919 respectively. It was shown that such an f exists if and only if the Pick matrix
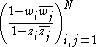
is positive semi-definite. Also, the function f is unique if and only if the Pick matrix has zero determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
. Pick's original proof was based on Blaschke product
Blaschke product
In complex analysis, the Blaschke product is a bounded analytic function in the open unit disc constructed to have zeros at a sequence of prescribed complex numbersinside the unit disc.Blaschke products were introduced by...
s.
Generalisation
It can be shown that the Hardy spaceHardy space
In complex analysis, the Hardy spaces Hp are certain spaces of holomorphic functions on the unit disk or upper half plane. They were introduced by Frigyes Riesz , who named them after G. H. Hardy, because of the paper...
H 2 is a reproducing kernel Hilbert space
Reproducing kernel Hilbert space
In functional analysis , a reproducing kernel Hilbert space is a Hilbert space of functions in which pointwise evaluation is a continuous linear functional. Equivalently, they are spaces that can be defined by reproducing kernels...
, and that its reproducing kernel (known as the Szegő
Gábor Szego
Gábor Szegő was a Hungarian mathematician. He was one of the foremost analysts of his generation and made fundamental contributions to the theory of Toeplitz matrices and orthogonal polynomials.-Life:...
kernel) is
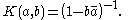
Because of this, the Pick matrix can be rewritten as
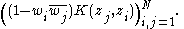
This description of the solution has motivated various attempts to generalise Nevanlinna and Pick's result.
The Nevanlinna–Pick problem can be generalised to that of finding a holomorphic function
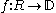that interpolates a given set of data, where R is now an arbitrary region of the complex plane.M. B. Abrahamse showed that if the boundary of R consists of finitely many analytic curves (say n + 1), then an interpolating function f exists if and only if
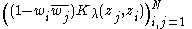
is a positive semi-definite matrix, for all λ in the n-torus. Here, the Kλs are the reproducing kernels corresponding to a particular set of reproducing kernel Hilbert spaces, which are related to the set R. It can also be shown that f is unique if and only if one of the Pick matrices has zero determinant.