Neutrino theory of light - AbsoluteAstronomy.com

The neutrino theory of light is the proposal that the photon

Photon

In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...

is a composite particle formed of a neutrino

Neutrino

A neutrino is an electrically neutral, weakly interacting elementary subatomic particle with a half-integer spin, chirality and a disputed but small non-zero mass. It is able to pass through ordinary matter almost unaffected...

-antineutrino pair

Pair production

Pair production refers to the creation of an elementary particle and its antiparticle, usually from a photon . For example an electron and its antiparticle, the positron, may be created...

. It is based on the idea that emission and absorption

Absorption (electromagnetic radiation)

In physics, absorption of electromagnetic radiation is the way by which the energy of a photon is taken up by matter, typically the electrons of an atom. Thus, the electromagnetic energy is transformed to other forms of energy for example, to heat. The absorption of light during wave propagation is...

of a photon corresponds to the creation and annihilation of a particle-antiparticle pair. The neutrino

Neutrino

theory of light is not currently accepted as part of mainstream physics, as according to the standard model

Standard Model

The Standard Model of particle physics is a theory concerning the electromagnetic, weak, and strong nuclear interactions, which mediate the dynamics of the known subatomic particles. Developed throughout the mid to late 20th century, the current formulation was finalized in the mid 1970s upon...

the photon is an elementary particle

Elementary particle

In particle physics, an elementary particle or fundamental particle is a particle not known to have substructure; that is, it is not known to be made up of smaller particles. If an elementary particle truly has no substructure, then it is one of the basic building blocks of the universe from which...

, a gauge boson

Gauge boson

In particle physics, gauge bosons are bosonic particles that act as carriers of the fundamental forces of nature. More specifically, elementary particles whose interactions are described by gauge theory exert forces on each other by the exchange of gauge bosons, usually as virtual particles.-...

.

Historically, many particles that were once thought to be elementary such as protons, neutrons, pions, and kaons have turned out to be composite particles. In 1932, Louis de Broglie suggested that the photon might be the combination of a neutrino and an antineutrino. During the 1930s there was great interest in the neutrino theory of light and Pascual Jordan

Pascual Jordan

-Further reading:...

, Ralph Kronig

Ralph Kronig

Ralph Kronig was a German-American physicist . He is noted for the discovery of particle spin and for his theory of x-ray absorption spectroscopy...

, Max Born

Max Born

Max Born was a German-born physicist and mathematician who was instrumental in the development of quantum mechanics. He also made contributions to solid-state physics and optics and supervised the work of a number of notable physicists in the 1920s and 30s...

, and others worked on the theory.

In 1938, Maurice Henry Lecorney Pryce brought work on the composite photon theory to halt. He showed that the conditions imposed by Bose-Einstein commutation relations for the composite photon and the connection between its spin and polarization were incompatible. Pryce also pointed out other possible problems, “In so far as the failure of the theory can be traced to any one cause it is fair to say that it lies in the fact that light waves are polarized transversely while neutrino ‘waves’ are polarized longitudinally,” and lack of rotational invariance. In 1966, V S Berezinskii reanalyzed Pryce’s paper, giving a clearer picture of the problem that Pryce uncovered.

Starting in the 1960s work on the neutrino theory of light resumed, and there continues to be some interest in recent years. Attempts have been made to solve the problem pointed out by Pryce, known as Pryce’s Theorem, and other problems with the composite photon theory. The incentive is seeing the natural way that many photon properties are generated from the theory and the knowledge that some problems exist with the current photon model. However, there is no experimental evidence that the photon has a composite structure.

Some of the problems for the neutrino theory of light are the non-existence for massless neutrinos with both spin parallel and antiparallel to their momentum and the fact that composite photons are not bosons. Attempts to solve some of these problems will be discussed, but the lack of massless neutrinos makes it impossible to form a massless photon with this theory. The neutrino theory of light is not considered to be part of mainstream

Standard Model

physics.

Forming photon from neutrinos

Actually, it is not difficult to obtain transversely polarized
photons from neutrinos.

The neutrino field

The neutrino field satisfies the Dirac equation

Dirac equation

The Dirac equation is a relativistic quantum mechanical wave equation formulated by British physicist Paul Dirac in 1928. It provided a description of elementary spin-½ particles, such as electrons, consistent with both the principles of quantum mechanics and the theory of special relativity, and...

with the mass set to zero,

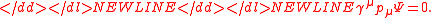
The gamma matrices in the Weyl basis are:

The matrix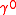

is Hermitian while

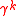is antihermitian. They satisfy the anticommutation relation,

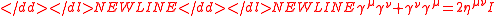
where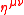

is the Minkowski metric with signature

and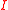

is the unit matrix.

The neutrino field is given by,

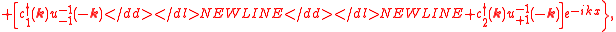
where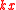

stands for

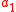and

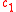are the fermion annihilation operators for

and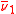

respectively, while

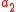and

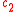are
the annihilation operators for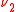

and

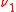is a right-handed neutrino and

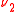is a left-handed neutrino.
The

's are spinors with the superscripts and subscripts referring to the energy and helicity states respectively. Spinor

Spinor

In mathematics and physics, in particular in the theory of the orthogonal groups , spinors are elements of a complex vector space introduced to expand the notion of spatial vector. Unlike tensors, the space of spinors cannot be built up in a unique and natural way from spatial vectors...

solutions for the Dirac equation

Dirac equation

are,

The neutrino spinors for negative momenta are related to those of positive momenta by,

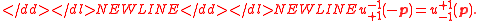
The composite photon field

De Broglie and Kronig suggested the use of a local interaction to bind the neutrino-antineutrino pair. (Rosen and Singer
have used a delta-function interaction in forming a
composite photon.)
Fermi and Yang
used a local interaction to bind
a fermion-antiferminon pair in attempting to form a pion. A four-vector field can be created from a fermion-antifermion pair,

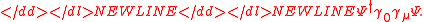
Forming the photon field can be done simply by,

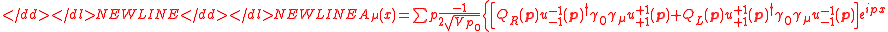
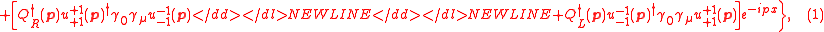
where

.

The annihilation operators for right-handed and left-handed photons formed of fermion-antifermion pairs are defined as,

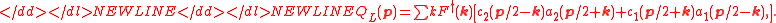
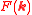is a spectral function, normalized by

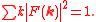
Photon polarization vectors

The polarization vectors corresponding to the combinations used
in Eq. (1) are,

Carrying out the matrix multiplications results in,

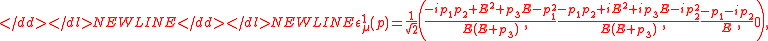
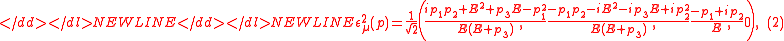
where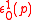

and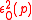

have been placed on the right.

For massless fermions the polarization vectors depend only upon the direction of

. Let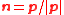

These polarization vectors satisfy the
normalization relation,

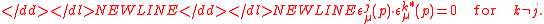
The Lorentz-invariant dot
products of the internal four-momentum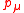

with the polarization vectors are,

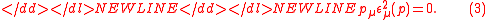
In three dimensions,

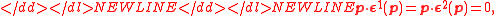
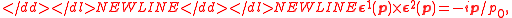
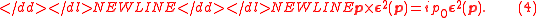
Composite photon satisfies Maxwell’s equations

In terms of the polarization vectors,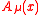

becomes,

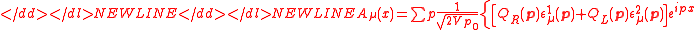
The electric field

and magnetic field

are given by,

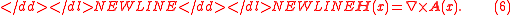
Applying Eq. (6) to Eq. (5), results in,

Maxwell's equations

Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...

for free space are obtained as follows:

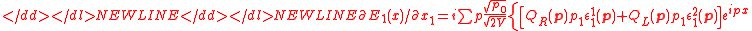
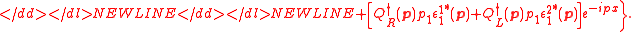
Thus,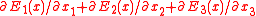

contains terms of the form

which equate to zero by the first of Eq. (4).
This gives,

contains similar terms.

The expression

contains terms of the form

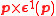while

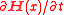
contains terms of form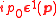

. Thus, the last two equations of (4) can be used to show that,

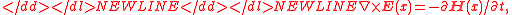
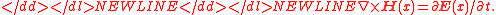
Although the neutrino field violates parity

Parity (physics)

In physics, a parity transformation is the flip in the sign of one spatial coordinate. In three dimensions, it is also commonly described by the simultaneous flip in the sign of all three spatial coordinates:...

and charge
conjugation
,

and

transform in the usual way
,

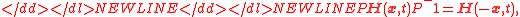
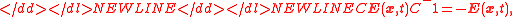
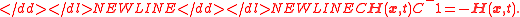
satisfies the Lorentz condition,

which follows from Eq. (3).

Although many choices for gamma matrices can satisfy the Dirac equation

Dirac equation

, it
is essential that one use the Weyl representation in order to get the correct photon polarization vectors and

and

that satisfy Maxwell's equations

Maxwell's equations

. Kronig
first realized this. In the Weyl representation,
the four-component spinors are describing two sets of two-component neutrinos.
The connection between the photon antisymmetric tensor and the two-component Weyl equation was also noted by Sen.
One can also produce the above results using a two-component neutrino theory.

To compute the commutation relations for the photon field,
one needs the equation,

To obtain this equation, Kronig
wrote a relation between the neutrino spinors that was not
rotationally invariant as pointed out by Pryce.
However, as Perkins showed, this equation
follows directly from summing over the polarization vectors,
Eq. (2), that were obtained by
explicitly solving for the neutrino spinors.

If the momentum is along the third axis,

and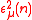

reduce to the usual polarization vectors
for right and left circularly polarized photons respectively.

Problems with the neutrino theory of light

Although composite photons satisfy many properties of real photons,
there are major problems with this theory.

Bose–Einstein commutation relations

It is known that a photon is a boson.
Does the composite photon satisfy Bose–Einstein commutation relations? Fermions are defined as the particles whose creation and annihilation operators adhere to the anticommutation relations

while bosons are defined as the particles that adhere to the commutation relations

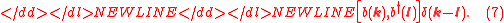
The creation and annihilation operators of composite particles formed of fermion pairs adhere to the commutation relations of the form

with

For Cooper electron pairs, "a" and "c" represent different spin directions. For nucleon pairs (the deuteron), "a" and "c" represent proton and neutron. For neutrino–antineutrino pairs, "a" and "c" represent neutrino and antineutrino. The size of the deviations from pure Bose behavior,

depends on the degree of overlap of the fermion wave functions and the constraints of the Pauli exclusion principle

Pauli exclusion principle

The Pauli exclusion principle is the quantum mechanical principle that no two identical fermions may occupy the same quantum state simultaneously. A more rigorous statement is that the total wave function for two identical fermions is anti-symmetric with respect to exchange of the particles...

.

If the state has the form

then the expectation value of Eq. (9) vanishes for

, and the expression for

can be approximated by

Using the fermion number operators

and

, this can be written,

showing that it is the average number
of fermions in a particular state

averaged
over all states with weighting factors

and

Jordan’s attempt to solve problem

De Broglie did not address the problem of statistics for the composite photon. However, "Jordan considered the essential part of the problem was to construct Bose–Einstein amplitudes from Fermi–Dirac amplitudes", as Pryce noted. Jordan "suggested that it is not the interaction between neutrinos and antineutrinos that binds them together into photons, but rather the manner in which they interact with charged particles that leads to the simplified description of light in terms of photons."

Jordan's hypothesis eliminated the need for theorizing an unknown interaction, but his hypothesis that the neutrino and antineutrino are emitted in exactly the same direction seems rather artificial as noted by Fock.
His strong desire to obtain exact Bose–Einstein commutation relations for the composite photon led him to work with a scalar or longitudinally polarized photon. Greenberg and Wightman
have pointed out why the one-dimensional case works, but the three-dimensional case does not.

In 1928, Jordan noticed that commutation relations for
pairs of fermions were similar to those for bosons.
Compare Eq. (7) with Eq. (8).
From 1935 till 1937, Jordan, Kronig, and others
tried to obtain exact Bose–Einstein commutation
relations for the composite photon. Terms were added to the
commutation relations to cancel out the delta term in Eq. (8).
These terms corresponded to "simulated photons."
For example, the absorption of a photon of momentum

could
be simulated by a Raman effect in which a neutrino with momentum

is absorbed while another of another with opposite spin and
momentum

is emitted. (It is now known that single neutrinos or antineutrinos interact so weakly that they cannot simulate photons.)

Pryce’s theorem

In 1938, Pryce showed that one cannot obtain
both Bose–Einstein statistics

Bose–Einstein statistics

In statistical mechanics, Bose–Einstein statistics determines the statistical distribution of identical indistinguishable bosons over the energy states in thermal equilibrium.-Concept:...

and transversely-polarized photons from
neutrino-antineutrino pairs. Construction of transversely-polarized
photons is not the problem.
As Berezinski
noted, "The only actual difficulty is that the construction of a transverse
four-vector is incompatible with the requirement of statistics."
In some ways Berezinski gives a clearer picture of the
problem. A simple version of the proof is as follows:

The expectation values of the commutation relations for composite
right and left-handed photons are:

where

The deviation from Bose–Einstein statistics

Bose–Einstein statistics

In statistical mechanics, Bose–Einstein statistics determines the statistical distribution of identical indistinguishable bosons over the energy states in thermal equilibrium.-Concept:...

is caused by

and

, which are functions of the neutrino numbers operators.

Linear polarization photon operators are defined by

A particularly interesting commutation relation is,

which follows from (10) and (12).

For the composite photon to obey Bose–Einstein commutation relations, at the very least,

Pryce noted.
From Eq. (11) and Eq. (13) the
requirement is that

gives zero when applied to any state vector. Thus, all the coefficients of

and

,
etc. must vanish separately. This means

,
and the composite photon does not exist, completing the proof.

Perkins’ attempt to solve problem

Perkins
reasoned that the photon does
not have to obey Bose–Einstein commutation relations, because the non-Bose
terms are small and they may not cause any detectable effects.
Perkins
noted, "As presented in many quantum mechanics
texts it may appear that Bose statistics follow from basic principles, but it is really from the classical canonical formalism. This is not a reliable procedure as evidenced by the fact that it gives the completely wrong result for spin-1/2 particles." Furthermore,
"most integral spin particles (light mesons, strange mesons, etc.) are composite particles formed of quarks. Because of their underlying fermion structure, these integral spin particles are not fundamental bosons, but composite quasibosons. However, in the asymptotic limit, which generally applies, they are essentially bosons. For these particles, Bose commutation relations are just an approximation, albeit a very good one. There are some differences; bringing two of these composite particles close together will force their identical fermions to jump to excited states because of the Pauli exclusion principle

Pauli exclusion principle

."

Brzezinski in reaffirming Pryce's theorem argues
that commutation relation (14) is necessary for the
photon to be truly neutral. However, Perkins
has shown that a neutral photon in the usual sense can be
obtained without Bose–Einstein commutation relations.

The number operator for a composite photon is defined as

Lipkin
suggested for a rough estimate to assume
that

where

is a constant equal
to the number of states used to construct the wave packet

Wave packet

In physics, a wave packet is a short "burst" or "envelope" of wave action that travels as a unit. A wave packet can be analyzed into, or can be synthesized from, an infinite set of component sinusoidal waves of different wavenumbers, with phases and amplitudes such that they interfere...

.

Perkins
showed that the effect
of the composite photon’s
number operator acting on a state of

composite photons is,

using

.
This result differs from the usual
one because of the second term which is small for large

.
Normalizing in the
usual manner,

where

is the state of

composite photons having momentum

which is created
by applying

on the vacuum

times.
Note that,

which is the same result as obtained
with boson operators. The formulas in Eq. (15)
are similar to the usual ones with correction factors
that approach zero for large

Blackbody radiation

The main evidence indicating that photons are bosons comes from the Blackbody radiation experiments which are in agreement with Planck's distribution. Perkins calculated the photon distribution for Blackbody radiation using the second quantization method, but with a composite photon.

The atoms in the walls of the cavity are taken to be a two-level system with photons emitted from the upper level β and absorbed at the lower level α. The transition probability for emission of a photon is enhanced when n_p photons are present,

where the first of (15) has been used. The absorption is enhanced less since the second of (15) is used,

Using the equality,

of the transition rates, Eqs. (16) and (17) are combined to give,

The probability of finding the system with energy E is proportional to e^−E/kT according to Boltzmann's distribution law. Thus, the equilibrium between emission and absorption requires that,

with the photon energy

. Combining the last two equations results in,

with

. For

, this reduces to

This equation differs from Planck’s law because of the

term. For the conditions used in the Blackbody radiation experiments of Coblentz, Perkins estimates that , and the maximum deviation from Planck's law is less than one part in , which is too small to be detected.

Only left-handed neutrinos exist

Experimental results show that only left-handed neutrinos
and right-handed antineutrinos exist. Three sets of neutrinos
have been observed, one
that is connected with electrons, one
with muons, and one with tau leptons.

In the standard model the pion and muon decay modes are:
| || → || || + ||
|----
| || → || || + || || + ||
|}

To form a photon, which satisfies parity and charge
conjugation, two sets of two-component neutrinos
(i.e., right-handed and left-handed neutrinos) are needed.
Perkins (see Sec. VI of Ref.)
attempted to solve this problem by noting that the needed
two sets of two-component neutrinos would exist if the
positive muon is identified as
the particle and the negative muon as the
antiparticle. The reasoning is as follows: let ₁ be
the right-handed neutrino and ₂ the left-handed neutrino
with their corresponding antineutrinos (with opposite helicity).
The neutrinos involved in beta decay are ₂
and ₂, while those for π-μ decay are
₁ and ₁.
With this scheme the pion and muon decay modes are:
| || → || || + || ₁
|----
| || → || || + || ₂ || + || ₁
|}

Absence of massless neutrinos

There is convincing evidence that neutrinos have mass.
In experiments at the SuperKamiokande researchers
have discovered neutrino oscillations in which one flavor of
neutrino changed into another. This means that neutrinos have
non-zero mass.
Since massless neutrinos are needed to form a massless photon,
a composite photon is not possible.

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.