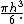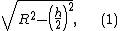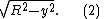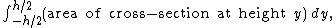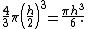Napkin ring problem
Encyclopedia
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, it is somewhat surprising that the volume of a band of specified height around a sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
—the part that remains after a hole in the shape of a circular cylinder is drilled through the sphere—does not depend on the sphere's radius
Radius
In classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...
.
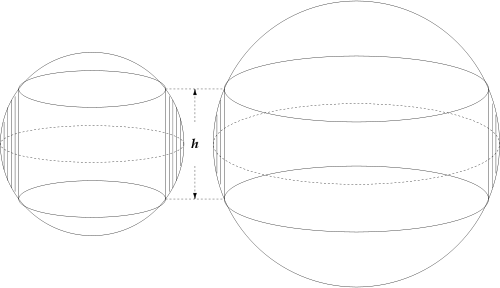
Specifically, suppose the axis of a right circular cylinder passes through the center of the sphere and the height (defined as distance in a direction parallel to the axis) of the part of the boundary of the cylinder that is inside the sphere is h, and the radius of the sphere is R. The "band" is the part of the sphere that is outside the cylinder.
The result is that the volume of the band depends on h but not on R.
As the radius R of the sphere shrinks, the diameter of the cylinder must also shrink in order that h can remain the same. The band gets thicker, and that would increase its volume. But it also gets shorter in circumference, and that would decrease its volume. The two effects exactly cancel each other out. The most extreme case, involving the smallest possible sphere, is that in which the diameter of the sphere is the same as the height h. In that case the volume of the band is the volume of the whole sphere:
An early study of this problem was written by 17th-century Japanese mathematician
Japanese mathematics
denotes a distinct kind of mathematics which was developed in Japan during the Edo Period . The term wasan, from wa and san , was coined in the 1870s and employed to distinguish native Japanese mathematics theory from Western mathematics .In the history of mathematics, the development of wasan...
Seki Kōwa. According to , Seki called this solid an arc-ring, or in Japanese
Japanese language
is a language spoken by over 130 million people in Japan and in Japanese emigrant communities. It is a member of the Japonic language family, which has a number of proposed relationships with other languages, none of which has gained wide acceptance among historical linguists .Japanese is an...
kokan or kokwan.
"Napkin Ring Problem" is called so because after removing cylinder from sphere the remaining band resembles shape of napkin ring.
Proof
Suppose the radius of the sphere is , the radius of the cylinder (or drill-bit) is
, the radius of the cylinder (or drill-bit) is 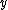 , and length of the cylinder (or the tunnel) is
, and length of the cylinder (or the tunnel) is 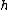 .
.By the Pythagorean theorem
Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
, the radius of the cylinder is
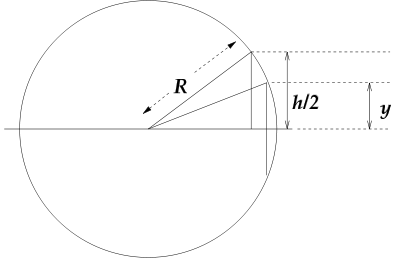
and the radius of the horizontal cross-section of the sphere at height y above the "equator" is
The cross-section of the band with the plane at height y is the region inside the larger circle of radius given by (2) and outside the smaller circle of radius given by (1). The cross-section's area is therefore the area of the larger circle minus the area of the smaller circle:
-
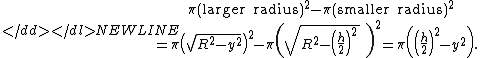
The radius R does not appear in the last quantity. Therefore the area of the horizontal cross-section at height y does not depend on R. The volume of the band is
and that does not depend on R.
This is an application of Cavalieri's principleCavalieri's principleIn geometry, Cavalieri's principle, sometimes called the method of indivisibles, named after Bonaventura Cavalieri, is as follows:* 2-dimensional case: Suppose two regions in a plane are included between two parallel lines in that plane...
: volumes with equal-sized corresponding cross-sections are equal. Indeed, the area of the cross-section is the same as that of the corresponding cross-section of a sphere of radius h/2, which has volume
-