Myhill–Nerode theorem
Encyclopedia
In the theory of formal language
s, the Myhill–Nerode theorem provides a necessary and sufficient condition
for a language to be regular
. The theorem is named for John Myhill
and Anil Nerode
, who proved it at the University of Chicago
in 1958 .
exactly one of the two strings xz and yz belongs to L.
Define a relation RL on strings by the rule that x RL y if there is no distinguishing extension for x and y. It is easy to show that RL is an equivalence relation
on strings, and thus it divides the set of all finite strings into equivalence classes.
The Myhill–Nerode Theorem states that L is regular if and only if RL has a finite number of equivalence classes, and moreover that the number of states in the smallest deterministic finite automaton (DFA) recognizing L is equal to the number of equivalence classes in RL. In particular, this implies that there is a unique canonical DFA
with minimum number of states.
The intuition is that if one starts with such a minimal automaton, then any strings x and y that drive it to the same state will be in the same equivalence class; and if one starts with a partition into equivalence classes, one can easily construct an automaton that uses its state to keep track of the equivalence class containing the part of the string seen so far.
Proof. First, suppose
where is the empty word on A . Construct a DFA =QAq0F (called the Nerode automaton for L ) with :QAQ defined by
(1)
(qa)=[wa]Lwq
and
(2)
F=qQwLwq
Then is well defined because w1Lw2 implies w1uLw2u . It is also straightforward that recognizes L .
On the other hand, let =QAq0F be a DFA that recognizes L . Extend to QA by putting (q)=q and (qaw)=((qa)w) for every qQ , aA , wA . Define f:QAL as
$\displaystyle f(q) = \left\{\begin{array}{ll} [w]_{\mathcal{N}_L} & \mathrm{if}... ...ptyset & \mathrm{if}\;\delta(q_0,w)\neq q\forall w\in A^\ast \end{array}\right.$ (1)
Then f is well defined. In fact, suppose q1=q2=q : then either f(q1)=f(q2)= , or there are w1w2A such that (q0w1)=(q0w2)=q . But in the latter case, (q0w1u)=(q0w2u)=(qu) for any uA , hence w1Lw2 since recognizes L . Finally, for any wA we have
so every class of L has a preimage according to f ; consequently, QAL .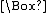 
by proving that the number of equivalence classes of RL is finite. This may be done by an exhaustive case analysis
in which, beginning from the empty string
, distinguishing extensions are used to find additional equivalence classes until no more can be found. For example, the language consisting of binary numbers which can be divided by 3 is regular. Given the empty string, 00 (or 11), 01 and 10 are distinguished extensions resulting in the three classes (corresponding to numbers that give remainders 0, 1 and 2 when divided by 3), but after this step there is no distinguished extension anymore. The minimal automaton accepting our language would have three states corresponding to these three equivalence classes.
Another immediate corollary
of the theorem is that if a language defines an infinite set of equivalence classes, it is not regular. It is this corollary that is frequently used to prove that a language is not regular.
Formal language
A formal language is a set of words—that is, finite strings of letters, symbols, or tokens that are defined in the language. The set from which these letters are taken is the alphabet over which the language is defined. A formal language is often defined by means of a formal grammar...
s, the Myhill–Nerode theorem provides a necessary and sufficient condition
Necessary and sufficient conditions
In logic, the words necessity and sufficiency refer to the implicational relationships between statements. The assertion that one statement is a necessary and sufficient condition of another means that the former statement is true if and only if the latter is true.-Definitions:A necessary condition...
for a language to be regular
Regular language
In theoretical computer science and formal language theory, a regular language is a formal language that can be expressed using regular expression....
. The theorem is named for John Myhill
John Myhill
John R. Myhill was a mathematician, born in 1923. He received his Ph.D. from Harvard University under Willard Van Orman Quine in 1949. He was professor at SUNY Buffalo from 1966 until his death in 1987...
and Anil Nerode
Anil Nerode
Anil Nerode is a U.S. mathematician, born in 1932. He received his undergraduate education and a Ph.D. in mathematics from the University of Chicago, the latter under the directions of Saunders Mac Lane. He enrolled in the Hutchins College at the University of Chicago in 1947 at the age of 15, and...
, who proved it at the University of Chicago
University of Chicago
The University of Chicago is a private research university in Chicago, Illinois, USA. It was founded by the American Baptist Education Society with a donation from oil magnate and philanthropist John D. Rockefeller and incorporated in 1890...
in 1958 .
Statement of the theorem
Given a language L, and a pair of strings x and y, define a distinguishing extension to be a string z such thatexactly one of the two strings xz and yz belongs to L.
Define a relation RL on strings by the rule that x RL y if there is no distinguishing extension for x and y. It is easy to show that RL is an equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
on strings, and thus it divides the set of all finite strings into equivalence classes.
The Myhill–Nerode Theorem states that L is regular if and only if RL has a finite number of equivalence classes, and moreover that the number of states in the smallest deterministic finite automaton (DFA) recognizing L is equal to the number of equivalence classes in RL. In particular, this implies that there is a unique canonical DFA
Dfa minimization
In computer science, more specifically in the branch of automata theory, DFA minimization is the task of transforming a given deterministic finite automaton into an equivalent DFA that has minimum number of states. Here, two DFAs are called equivalent if they describe the same regular language...
with minimum number of states.
The intuition is that if one starts with such a minimal automaton, then any strings x and y that drive it to the same state will be in the same equivalence class; and if one starts with a partition into equivalence classes, one can easily construct an automaton that uses its state to keep track of the equivalence class containing the part of the string seen so far.
Proof. First, suppose
where is the empty word on A . Construct a DFA =QAq0F (called the Nerode automaton for L ) with :QAQ defined by(1)
(qa)=[wa]Lwq
and
(2)
F=qQwLwq
Then is well defined because w1Lw2 implies w1uLw2u . It is also straightforward that recognizes L .
On the other hand, let =QAq0F be a DFA that recognizes L . Extend to QA by putting (q)=q and (qaw)=((qa)w) for every qQ , aA , wA . Define f:QAL as
$\displaystyle f(q) = \left\{\begin{array}{ll} [w]_{\mathcal{N}_L} & \mathrm{if}... ...ptyset & \mathrm{if}\;\delta(q_0,w)\neq q\forall w\in A^\ast \end{array}\right.$ (1)
Then f is well defined. In fact, suppose q1=q2=q : then either f(q1)=f(q2)= , or there are w1w2A such that (q0w1)=(q0w2)=q . But in the latter case, (q0w1u)=(q0w2u)=(qu) for any uA , hence w1Lw2 since recognizes L . Finally, for any wA we have
so every class of L has a preimage according to f ; consequently, QAL . 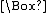Use and consequences
The Myhill–Nerode theorem may be used to show that a language L is regularRegular language
In theoretical computer science and formal language theory, a regular language is a formal language that can be expressed using regular expression....
by proving that the number of equivalence classes of RL is finite. This may be done by an exhaustive case analysis
Case analysis
Case analysis is one of the most general and applicable methods of analytical thinking, depending only on the division of a problem, decision or situation into a sufficient number of separate cases. Analysing each such case individually may be enough to resolve the initial question...
in which, beginning from the empty string
Empty string
In computer science and formal language theory, the empty string is the unique string of length zero. It is denoted with λ or sometimes Λ or ε....
, distinguishing extensions are used to find additional equivalence classes until no more can be found. For example, the language consisting of binary numbers which can be divided by 3 is regular. Given the empty string, 00 (or 11), 01 and 10 are distinguished extensions resulting in the three classes (corresponding to numbers that give remainders 0, 1 and 2 when divided by 3), but after this step there is no distinguished extension anymore. The minimal automaton accepting our language would have three states corresponding to these three equivalence classes.
Another immediate corollary
Corollary
A corollary is a statement that follows readily from a previous statement.In mathematics a corollary typically follows a theorem. The use of the term corollary, rather than proposition or theorem, is intrinsically subjective...
of the theorem is that if a language defines an infinite set of equivalence classes, it is not regular. It is this corollary that is frequently used to prove that a language is not regular.