
Morphological skeleton
Encyclopedia
In digital image processing
, morphological skeleton is a skeleton
(or medial axis
) representation of a shape
or binary image
, computed by means of morphological operators
.
Morphological skeletons are of two kinds:
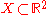 :
:
 ,
,
where and
and  are the morphological erosion
are the morphological erosion
and opening
, respectively, and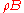 is an open ball of radius
is an open ball of radius
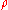 .
.
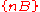 ,
, 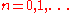 , be a family of shapes, where B is a structuring element
, be a family of shapes, where B is a structuring element
, , and
, and , where o denotes the origin.
, where o denotes the origin.
The variable n is called the size of the structuring element.
Lantuéjoul's formula has been discretized as follows. For a discrete binary image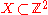 , the skeleton S(X) is the union of the skeleton subsets
, the skeleton S(X) is the union of the skeleton subsets 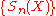 ,
, 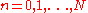 , where:
, where:
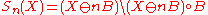 .
.
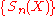 as follows:
as follows:
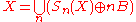 .
.
Partial reconstructions can also be performed, leading to opened versions of the original shape:
 .
.
 be the translated version version of
be the translated version version of 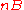 to the point z, that is,
to the point z, that is,  .
.
A shape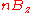 centered at z is called a maximal disk in a set A when:
centered at z is called a maximal disk in a set A when:
Each skeleton subset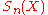 consists of the centers of all maximal disks of size n.
consists of the centers of all maximal disks of size n.
Digital image processing
Digital image processing is the use of computer algorithms to perform image processing on digital images. As a subcategory or field of digital signal processing, digital image processing has many advantages over analog image processing...
, morphological skeleton is a skeleton
Topological skeleton
In shape analysis, skeleton of a shape is a thin version of that shape that is equidistant to its boundaries. The skeleton usually emphasizes geometrical and topological properties of the shape, such as its connectivity, topology, length, direction, and width...
(or medial axis
Medial axis
The medial axis of an object is the set of all points having more than one closest point on the object's boundary. Originally referred to as the topological skeleton, it was introduced by Blum as a tool for biological shape recognition....
) representation of a shape
Shape
The shape of an object located in some space is a geometrical description of the part of that space occupied by the object, as determined by its external boundary – abstracting from location and orientation in space, size, and other properties such as colour, content, and material...
or binary image
Binary image
A binary image is a digital image that has only two possible values for each pixel. Typically the two colors used for a binary image are black and white though any two colors can be used. The color used for the object in the image is the foreground color while the rest of the image is the...
, computed by means of morphological operators
Mathematical morphology
Mathematical morphology is a theory and technique for the analysis and processing of geometrical structures, based on set theory, lattice theory, topology, and random functions...
.
Morphological skeletons are of two kinds:
- Those defined and by means of morphological openingOpening (morphology)In mathematical morphology, opening is the dilation of the erosion of a set A by a structuring element B:A\circ B = \oplus B, \, where \ominus and \oplus denote erosion and dilation, respectively....
s, from which the original shape can be reconstructed, - Those computed by means of the hit-or-miss transformHit-or-miss transformIn mathematical morphology, hit-or-miss transform is an operation that detects a given configuration in a binary image, using the morphological erosion operator and a pair of disjoint structuring elements...
, which preserve the shape's topologyTopologyTopology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
.
Continuous images
In (Lantuéjoul 1977), Lantuéjoul derived the following morphological formula for the skeleton of a continuous binary image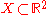 :
: ,
,where
 and
and  are the morphological erosion
are the morphological erosionErosion (morphology)
For use of "Erosion" in dermatopathology, see Erosion Erosion is one of two fundamental operations in Morphological image processing from which all other morphological operations are based...
and opening
Opening (morphology)
In mathematical morphology, opening is the dilation of the erosion of a set A by a structuring element B:A\circ B = \oplus B, \, where \ominus and \oplus denote erosion and dilation, respectively....
, respectively, and
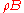 is an open ball of radius
is an open ball of radiusRadius
In classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...
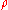 .
.Discrete images
Let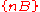 ,
, 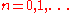 , be a family of shapes, where B is a structuring element
, be a family of shapes, where B is a structuring elementStructuring element
In mathematical morphology, a structuring element is a shape, used to probe or interact with a given image, with the purpose of drawing conclusions on how this shape fits or misses the shapes in the image...
,
 , and
, and , where o denotes the origin.
, where o denotes the origin.The variable n is called the size of the structuring element.
Lantuéjoul's formula has been discretized as follows. For a discrete binary image
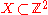 , the skeleton S(X) is the union of the skeleton subsets
, the skeleton S(X) is the union of the skeleton subsets 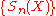 ,
, 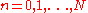 , where:
, where: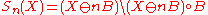 .
.Reconstruction from the skeleton
The original shape X can be reconstructed from the set of skeleton subsets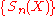 as follows:
as follows: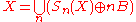 .
.Partial reconstructions can also be performed, leading to opened versions of the original shape:
 .
.The skeleton as the centers of the maximal disks
Let be the translated version version of
be the translated version version of 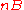 to the point z, that is,
to the point z, that is,  .
.A shape
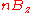 centered at z is called a maximal disk in a set A when:
centered at z is called a maximal disk in a set A when:
-
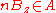 , and
, and - if, for some integer m and some point y,
 , then
, then  .
.
Each skeleton subset
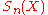 consists of the centers of all maximal disks of size n.
consists of the centers of all maximal disks of size n.

