Morlet wavelet
Encyclopedia
In mathematics
, the Morlet wavelet, named after Jean Morlet
, was originally formulated by Goupillaud, Grossmann and Morlet in 1984 as a constant
subtracted from a plane wave and then localised by a Gaussian
window:
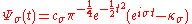
where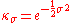
is defined by
the admissibility criterion and the normalisation constant
is:
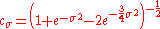
The Fourier transform
of the Morlet wavelet is:
The "central frequency"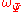
is the position of the global maximum of 
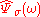which, in this case, is given by the solution of the equation:
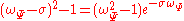
The parameter
in the Morlet wavelet allows trade between
time and frequency resolutions. Conventionally, the restriction
is used to avoid problems with the Morlet wavelet at low 
(high temporal resolution).
For signals containing only slowly varying frequency and amplitude
modulations (audio, for example) it is not necessary to use small
values of
. In this case,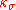 
becomes very small (e.g. 
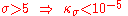) and is, therefore, often neglected. Under the restriction 
, the frequency of the Morlet wavelet is conventionally taken to be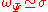 
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Morlet wavelet, named after Jean Morlet
Jean Morlet
Jean Morlet was a French geophysicist who pioneered work in the field of wavelet analysis around the year 1975. He invented the term wavelet to describe the functions he was using...
, was originally formulated by Goupillaud, Grossmann and Morlet in 1984 as a constant
subtracted from a plane wave and then localised by a GaussianGAUSSIAN
Gaussian is a computational chemistry software program initially released in 1970 by John Pople and his research group at Carnegie-Mellon University as Gaussian 70. It has been continuously updated since then...
window:
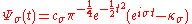
where
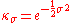is defined bythe admissibility criterion and the normalisation constant
is: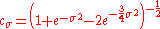The Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
of the Morlet wavelet is:
The "central frequency"
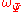is the position of the global maximum of 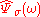which, in this case, is given by the solution of the equation: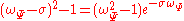The parameter
in the Morlet wavelet allows trade betweentime and frequency resolutions. Conventionally, the restriction
is used to avoid problems with the Morlet wavelet at low (high temporal resolution).For signals containing only slowly varying frequency and amplitude
modulations (audio, for example) it is not necessary to use small
values of
. In this case, 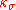becomes very small (e.g. 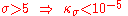) and is, therefore, often neglected. Under the restriction , the frequency of the Morlet wavelet is conventionally taken to be 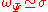.