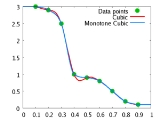
Monotone cubic interpolation
Encyclopedia
In the mathematical
subfield of numerical analysis
, monotone cubic interpolation is a variant of cubic interpolation that preserves monotonicity of the data set
being interpolated.
Monotonicity is preserved by linear interpolation
but not guaranteed by cubic interpolation.
 Monotone interpolation can be accomplished using cubic Hermite spline
Monotone interpolation can be accomplished using cubic Hermite spline
with the tangents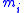 modified to ensure the monotonicity of the resulting Hermite spline.
modified to ensure the monotonicity of the resulting Hermite spline.
Let the data points be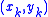 for
for 
Note that only one pass of the algorithm is required.
, using the data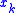 ,
, 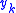 , and
, and 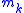 for
for 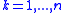 .
.
To evaluate at , find the smallest value larger than
, find the smallest value larger than  ,
,  , and the largest value smaller than
, and the largest value smaller than  ,
, 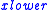 , among
, among 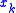 such that
such that  . Calculate
. Calculate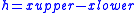 and
and 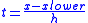
then the interpolant is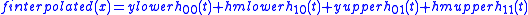
where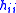 are the basis functions for the cubic Hermite spline
are the basis functions for the cubic Hermite spline
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
subfield of numerical analysis
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
, monotone cubic interpolation is a variant of cubic interpolation that preserves monotonicity of the data set
Data set
A data set is a collection of data, usually presented in tabular form. Each column represents a particular variable. Each row corresponds to a given member of the data set in question. Its values for each of the variables, such as height and weight of an object or values of random numbers. Each...
being interpolated.
Monotonicity is preserved by linear interpolation
Linear interpolation
Linear interpolation is a method of curve fitting using linear polynomials. Lerp is an abbreviation for linear interpolation, which can also be used as a verb .-Linear interpolation between two known points:...
but not guaranteed by cubic interpolation.
Monotone cubic Hermite interpolation

Cubic Hermite spline
In the mathematical subfield of numerical analysis a cubic Hermite spline , named in honor of Charles Hermite, is a third-degree spline with each polynomial of the spline in Hermite form...
with the tangents
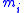 modified to ensure the monotonicity of the resulting Hermite spline.
modified to ensure the monotonicity of the resulting Hermite spline.Interpolant selection
There are several ways of selecting interpolating tangents for each data point. This section will outline the use of the Fritsch–Carlson method.Let the data points be
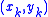 for
for 
- Compute the slopes of the secant lineSecant lineA secant line of a curve is a line that intersects two points on the curve. The word secant comes from the Latin secare, to cut.It can be used to approximate the tangent to a curve, at some point P...
s between successive points:
for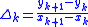
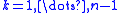 .
. - Initialize the tangents at every data point as the average of the secants,
for
 ; these may be updated in further steps. For the endpoints, use one-sided differences:
; these may be updated in further steps. For the endpoints, use one-sided differences: 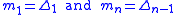
- For
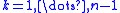 , if
, if 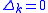 (if two successive
(if two successive  are equal), then set
are equal), then set 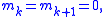 as the spline connecting these points must be flat to preserve monotonicity. Ignore step 4 and 5 for those
as the spline connecting these points must be flat to preserve monotonicity. Ignore step 4 and 5 for those  .
. - Let
 and
and 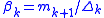 . If
. If  or
or  are computed to be zero, then the input data points are not strictly monotone. In such cases, piecewise monotone curves can still be generated by choosing
are computed to be zero, then the input data points are not strictly monotone. In such cases, piecewise monotone curves can still be generated by choosing  , although global strict monotonicity is not possible.
, although global strict monotonicity is not possible. - To prevent overshootOvershootOvershoot may refer to:* Overshoot , when a signal exceeds its steady state value* Overshoot , when a population exceeds the environment's carrying capacity* Overshoot , an aborted landing...
and ensure monotonicity, the function
must have a value greater than (or equal to, if monotonicity need not be strict) zero. One simple way to satisfy this constraint is to restrict the magnitude of vector
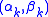 to a circle of radius 3. That is, if
to a circle of radius 3. That is, if 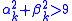 , then set
, then set 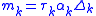 and
and 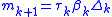 where
where 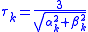 .
.
Note that only one pass of the algorithm is required.
Cubic interpolation
After the preprocessing, evaluation of the interpolated spline is equivalent to cubic Hermite splineCubic Hermite spline
In the mathematical subfield of numerical analysis a cubic Hermite spline , named in honor of Charles Hermite, is a third-degree spline with each polynomial of the spline in Hermite form...
, using the data
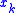 ,
, 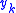 , and
, and 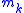 for
for 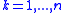 .
.To evaluate at
 , find the smallest value larger than
, find the smallest value larger than  ,
,  , and the largest value smaller than
, and the largest value smaller than  ,
, 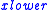 , among
, among 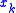 such that
such that  . Calculate
. Calculate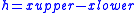 and
and 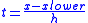
then the interpolant is
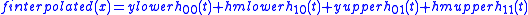
where
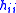 are the basis functions for the cubic Hermite spline
are the basis functions for the cubic Hermite splineCubic Hermite spline
In the mathematical subfield of numerical analysis a cubic Hermite spline , named in honor of Charles Hermite, is a third-degree spline with each polynomial of the spline in Hermite form...
.
External links
- GPLv3 licensed C++C++C++ is a statically typed, free-form, multi-paradigm, compiled, general-purpose programming language. It is regarded as an intermediate-level language, as it comprises a combination of both high-level and low-level language features. It was developed by Bjarne Stroustrup starting in 1979 at Bell...
implementation: MonotCubicInterpolator.cpp MonotCubicInterpolator.hpp

