
Monge's theorem
Encyclopedia
In geometry
, Monge's theorem, named after Gaspard Monge
, states that for any three circles in a plane, none of which is inside one of the others, the three intersection points of the three pairs of external tangent lines are in fact collinear
.
(For any two circles in a plane, an external tangent is a line that is tangent to both circles
but does not pass between them. There are two such external tangent lines for any two circles. In other words the two lines which form an "ice-cream cone" which "holds" the two circles.)
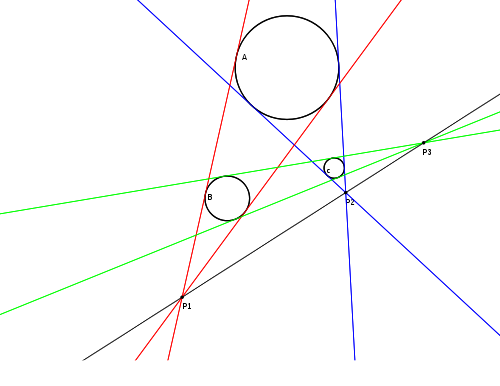
Monge's theorem lets us know that surprisingly the three "points" of the "ice-cream cones" are always in a straight line. In the visual example below the red, green, and blue points are all in a straight line.
(In the case of two of the circles being of equal size: the two external tangent lines are of course parallel. In this case Monge's theorem asserts that the other two intersection points must lie on a line parallel to those two external tangents. In other words if the two external tangents are considered to intersect at the point at infinity, then the other two intersection points must be on a line passing through the same point at infinity.)
Monge's theorem can also be proved by using Desargues' theorem
.
Another easy proof is using Menelaus' theorem
, since the ratios can be calculated with the diameters of each circle, which will be eliminated by cyclic forms when using the Menelaus' theorem
.
Desargues' theorem also asserts that 3 points lie on a line, and has a similar proof using the same idea of considering it in 3 rather than 2 dimensions and writing the line as an intersection of 2 planes.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, Monge's theorem, named after Gaspard Monge
Gaspard Monge
Gaspard Monge, Comte de Péluse was a French mathematician, revolutionary, and was inventor of descriptive geometry. During the French Revolution, he was involved in the complete reorganization of the educational system, founding the École Polytechnique...
, states that for any three circles in a plane, none of which is inside one of the others, the three intersection points of the three pairs of external tangent lines are in fact collinear
Line (geometry)
The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
.
(For any two circles in a plane, an external tangent is a line that is tangent to both circles
Tangent lines to circles
In Euclidean plane geometry, tangent lines to circles form the subject of several theorems, and play an important role in many geometrical constructions and proofs...
but does not pass between them. There are two such external tangent lines for any two circles. In other words the two lines which form an "ice-cream cone" which "holds" the two circles.)
Monge's theorem lets us know that surprisingly the three "points" of the "ice-cream cones" are always in a straight line. In the visual example below the red, green, and blue points are all in a straight line.
(In the case of two of the circles being of equal size: the two external tangent lines are of course parallel. In this case Monge's theorem asserts that the other two intersection points must lie on a line parallel to those two external tangents. In other words if the two external tangents are considered to intersect at the point at infinity, then the other two intersection points must be on a line passing through the same point at infinity.)

Proofs
The simplest proof employs a three-dimensional analogy. Let the three circles correspond to three spheres of the same radii; the circles correspond to the equators that result from a plane passing through the centers of the spheres. The three spheres can be sandwiched uniquely between two planes. Each pair of spheres defines a cone that is externally tangent to both spheres, and the apex of this cone corresponds to the intersection point of the two external tangents, i.e., the external homothetic center. Since one line of the cone lies in each plane, the apex of each cone must lie in both planes, and hence somewhere on the line of intersection of the two planes. Therefore, the three external homothetic centers are collinear.Monge's theorem can also be proved by using Desargues' theorem
Desargues' theorem
In projective geometry, Desargues' theorem, named in honor of Gérard Desargues, states:Denote the three vertices of one triangle by a, b, and c, and those of the other by A, B, and C...
.
Another easy proof is using Menelaus' theorem
Menelaus' theorem
Menelaus' theorem, named for Menelaus of Alexandria, is a theorem about triangles in plane geometry. Given a triangle ABC, and a transversal line that crosses BC, AC and AB at points D, E and F respectively, with D, E, and F distinct from A, B and C, thenThis equation uses signed lengths of...
, since the ratios can be calculated with the diameters of each circle, which will be eliminated by cyclic forms when using the Menelaus' theorem
Menelaus' theorem
Menelaus' theorem, named for Menelaus of Alexandria, is a theorem about triangles in plane geometry. Given a triangle ABC, and a transversal line that crosses BC, AC and AB at points D, E and F respectively, with D, E, and F distinct from A, B and C, thenThis equation uses signed lengths of...
.
Desargues' theorem also asserts that 3 points lie on a line, and has a similar proof using the same idea of considering it in 3 rather than 2 dimensions and writing the line as an intersection of 2 planes.
See also
- Homothetic centers of circles
- Problem of ApolloniusProblem of ApolloniusIn Euclidean plane geometry, Apollonius' problem is to construct circles that are tangent to three given circles in a plane . Apollonius of Perga posed and solved this famous problem in his work ; this work has been lost, but a 4th-century report of his results by Pappus of Alexandria has survived...
, constructs a circle (not necessarily unique) given three other circles
External links
- Monge's Circle Theorem at MathWorldMathWorldMathWorld is an online mathematics reference work, created and largely written by Eric W. Weisstein. It is sponsored by and licensed to Wolfram Research, Inc. and was partially funded by the National Science Foundation's National Science Digital Library grant to the University of Illinois at...
- Monge's theorem at cut-the-knotCut-the-knotCut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...
- Three Circles and Common Tangents at cut-the-knotCut-the-knotCut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...

