
Minkowski's first inequality for convex bodies
Encyclopedia
In mathematics
, Minkowski's first inequality for convex bodies is a geometrical result due to the German
mathematician
Hermann Minkowski
. The inequality is closely related to the Brunn–Minkowski inequality and the isoperimetric inequality.
al convex bodies
in n-dimensional Euclidean space
Rn. Define a quantity V1(K, L) by
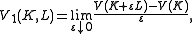
where V denotes the n-dimensional Lebesgue measure
and + denotes the Minkowski sum. Then
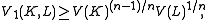
with equality if and only if
K and L are homothetic, i.e. are equal up to translation
and dilation
.
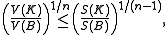
with equality if and only if K is a ball of some radius.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Minkowski's first inequality for convex bodies is a geometrical result due to the German
Germany
Germany , officially the Federal Republic of Germany , is a federal parliamentary republic in Europe. The country consists of 16 states while the capital and largest city is Berlin. Germany covers an area of 357,021 km2 and has a largely temperate seasonal climate...
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Hermann Minkowski
Hermann Minkowski
Hermann Minkowski was a German mathematician of Ashkenazi Jewish descent, who created and developed the geometry of numbers and who used geometrical methods to solve difficult problems in number theory, mathematical physics, and the theory of relativity.- Life and work :Hermann Minkowski was born...
. The inequality is closely related to the Brunn–Minkowski inequality and the isoperimetric inequality.
Statement of the inequality
Let K and L be two n-dimensionDimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
al convex bodies
Convex body
In mathematics, a convex body in n-dimensional Euclidean space Rn is a compact convex set with non-empty interior.A convex body K is called symmetric if it is centrally symmetric with respect to the origin, i.e. a point x lies in K if and only if its antipode, −x, also lies in K...
in n-dimensional Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
Rn. Define a quantity V1(K, L) by
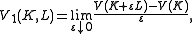
where V denotes the n-dimensional Lebesgue measure
Lebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
and + denotes the Minkowski sum. Then
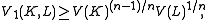
with equality if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
K and L are homothetic, i.e. are equal up to translation
Translation (geometry)
In Euclidean geometry, a translation moves every point a constant distance in a specified direction. A translation can be described as a rigid motion, other rigid motions include rotations and reflections. A translation can also be interpreted as the addition of a constant vector to every point, or...
and dilation
Dilation (mathematics)
In mathematics, a dilation is a function f from a metric space into itself that satisfies the identityd=rd \,for all points where d is the distance from x to y and r is some positive real number....
.
Remarks
- V1 is just one example of a class of quantities known as mixed volumeMixed volumeIn mathematics, more specifically, in convex geometry, the mixed volume is a way to associate a non-negative number to an n-tuple of convex bodies in the n-dimensional space...
s. - If L is the n-dimensional unit ball B, then n V1(K, B) is the (n − 1)-dimensional surface measure of K, denoted S(K).
The Brunn–Minkowski inequality
One can show that the Brunn–Minkowski inequality for convex bodies in Rn implies Minkowski's first inequality for convex bodies in Rn, and that equality in the Brunn–Minkowski inequality implies equality in Minkowski's first inequality.The isoperimetric inequality
By taking L = B, the n-dimensional unit ball, in Minkowski's first inequality for convex bodies, one obtains the isoperimetric inequality for convex bodies in Rn: if K is a convex body in Rn, then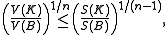
with equality if and only if K is a ball of some radius.

