Min-entropy
Encyclopedia
In probability theory
or information theory
, the min-entropy of a discrete random event x with possible states (or outcomes) 1... n and corresponding probabilities p1... pn is
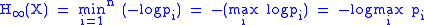
The base of the logarithm is just a scaling constant; for a result in bit
s, use a base-2 logarithm. Thus, a
distribution has a min-entropy of at least b bits if no possible state has a probability greater than 2-b.
The min-entropy is always less than or equal to the Shannon entropy; it is equal when all the probabilities pi are equal.
Min-entropy is important in the theory of randomness extractor
.
The notation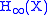
derives from a parameterized family of Shannon-like entropy measures, Rényi entropy
,
k=1 is the Shannon entropy. As k is increased, more weight is given to the larger probabilities, and in the limit as k→∞, only the largest p_i has any effect on the result.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
or information theory
Information theory
Information theory is a branch of applied mathematics and electrical engineering involving the quantification of information. Information theory was developed by Claude E. Shannon to find fundamental limits on signal processing operations such as compressing data and on reliably storing and...
, the min-entropy of a discrete random event x with possible states (or outcomes) 1... n and corresponding probabilities p1... pn is
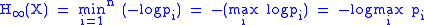
The base of the logarithm is just a scaling constant; for a result in bit
Bit
A bit is the basic unit of information in computing and telecommunications; it is the amount of information stored by a digital device or other physical system that exists in one of two possible distinct states...
s, use a base-2 logarithm. Thus, a
distribution has a min-entropy of at least b bits if no possible state has a probability greater than 2-b.
The min-entropy is always less than or equal to the Shannon entropy; it is equal when all the probabilities pi are equal.
Min-entropy is important in the theory of randomness extractor
Randomness extractor
A randomness extractor, often simply called "an extractor," is a function which, when applied to a high-entropy source , generates a random output that is shorter, but uniformly distributed...
.
The notation
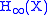derives from a parameterized family of Shannon-like entropy measures, Rényi entropyRényi entropy
In information theory, the Rényi entropy, a generalisation of Shannon entropy, is one of a family of functionals for quantifying the diversity, uncertainty or randomness of a system...
,
k=1 is the Shannon entropy. As k is increased, more weight is given to the larger probabilities, and in the limit as k→∞, only the largest p_i has any effect on the result.