Merkle signature scheme
Encyclopedia
The Merkle signature scheme is a digital signature scheme
based on hash trees (also called Merkle trees) and one-time signatures such as the Lamport signature scheme. It was developed by Ralph Merkle
in the late 70s and is an alternative to traditional digital signatures such as the Digital Signature Algorithm
or RSA. The advantage of the Merkle Signature Scheme is, that it is believed to be resistant against quantum computer
algorithms. The traditional public key algorithms, such as RSA and ELGamal would become insecure in case an effective quantum computer can be built (Shor's algorithm
). The Merkle Signature Scheme however only depends on the existence of secure hash function
s. This makes the Merkle Signature Scheme very adjustable and resistant against quantum computing.
The Merkle Signature Scheme can only be used to sign a limited number of messages with one public key 
. The number of possible messages must be a power of two, so that we denote the possible number of messages as 
.
The first step of generating the public key
is to generate the public keys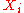 
and private keys 
of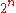 
one-time signatures. For each private key 
, with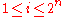 
, a hash value 
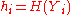is computed. With these hash values 
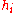a hash tree
is built.
We call a node of the tree
, where 
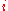denotes the level of the node. The level of a node is defined by the distance from the node to a leaf. Hence, a leaf of the tree has level 
and the root has level 
. We number all nodes of one level from the left to the right, so that 
is the leftmost node of level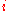 
.
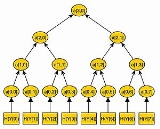
In the Merkle Tree the hash values
are the leaves of a binary tree, so that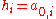 
. Each inner node of the tree is the hash value of the concatenation of its two children. So 
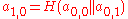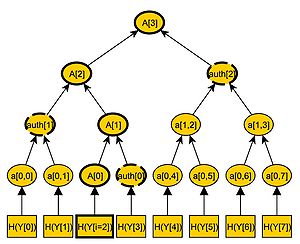
and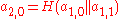 
. An example of a merkle tree is illustrated in figure \ref{fig:gra1}.
In this way, a tree with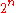
leaves and 
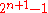nodes is built. The root of the tree 
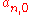is the public key 
of the Merkle Signature Scheme.
To sign a message 
with the Merkle Signature Scheme, the message 
is signed with a one-time signature scheme, resulting in a signature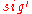 
, first. This is done, by using one of the public and private key pairs 
.
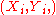The corresponding leaf of the hash tree to a one-time public key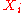
is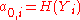 
. We call the path in the hash tree from 
to the root 
. The path 
consists of 
nodes, 
, with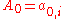 
being the leaf and 
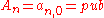being the root of the tree. To compute this path 
, we need every child of the nodes 
. We know that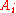 
is a child of 
. To calculate the next node 
of the path 
, we need to know both children of 
. So we need the brother node of 
. We call this node 
, so that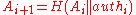 
. Hence, 
nodes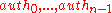 
are needed, to compute every node of the path 
. We now calculate and save these nodes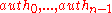 
.
These nodes, plus the one-time signature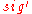
of 
is the signature 
of the Merkle Signature Scheme. An example of an authentication path is illustrated in the figure on the right.
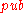, the message 
, and the signature 
. At first, the receiver verifies the one-time signature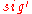 
of the message 
. If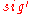 
is a valid signature of 
, the receiver computes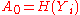 
by hashing the public key of the one-time signature. For 
, the nodes of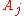 
of the path 
are computed with 
. If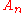 
equals the public key 
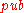of the merkle signature scheme, the signature is valid.
Digital signature
A digital signature or digital signature scheme is a mathematical scheme for demonstrating the authenticity of a digital message or document. A valid digital signature gives a recipient reason to believe that the message was created by a known sender, and that it was not altered in transit...
based on hash trees (also called Merkle trees) and one-time signatures such as the Lamport signature scheme. It was developed by Ralph Merkle
Ralph Merkle
Ralph C. Merkle is a researcher in public key cryptography, and more recently a researcher and speaker on molecular nanotechnology and cryonics...
in the late 70s and is an alternative to traditional digital signatures such as the Digital Signature Algorithm
Digital Signature Algorithm
The Digital Signature Algorithm is a United States Federal Government standard or FIPS for digital signatures. It was proposed by the National Institute of Standards and Technology in August 1991 for use in their Digital Signature Standard , specified in FIPS 186, adopted in 1993. A minor...
or RSA. The advantage of the Merkle Signature Scheme is, that it is believed to be resistant against quantum computer
Quantum computer
A quantum computer is a device for computation that makes direct use of quantum mechanical phenomena, such as superposition and entanglement, to perform operations on data. Quantum computers are different from traditional computers based on transistors...
algorithms. The traditional public key algorithms, such as RSA and ELGamal would become insecure in case an effective quantum computer can be built (Shor's algorithm
Shor's algorithm
Shor's algorithm, named after mathematician Peter Shor, is a quantum algorithm for integer factorization formulated in 1994...
). The Merkle Signature Scheme however only depends on the existence of secure hash function
Hash function
A hash function is any algorithm or subroutine that maps large data sets to smaller data sets, called keys. For example, a single integer can serve as an index to an array...
s. This makes the Merkle Signature Scheme very adjustable and resistant against quantum computing.
Key generation
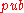. The number of possible messages must be a power of two, so that we denote the possible number of messages as .The first step of generating the public key
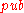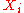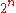is to generate the public keys and private keys of one-time signatures. For each private key , with 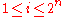, a hash value 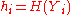is computed. With these hash values 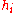a hash treeHash tree
In cryptography and computer science Hash trees or Merkle trees are a type of data structure which contains a tree of summary information about a larger piece of data – for instance a file – used to verify its contents. Hash trees are a combination of hash lists and hash chaining, which in turn are...
is built.
We call a node of the tree
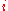, where denotes the level of the node. The level of a node is defined by the distance from the node to a leaf. Hence, a leaf of the tree has level and the root has level . We number all nodes of one level from the left to the right, so that is the leftmost node of level 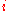.In the Merkle Tree the hash values
are the leaves of a binary tree, so that 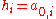. Each inner node of the tree is the hash value of the concatenation of its two children. So 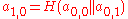and 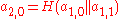. An example of a merkle tree is illustrated in figure \ref{fig:gra1}.In this way, a tree with
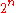leaves and 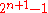nodes is built. The root of the tree 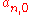is the public key of the Merkle Signature Scheme.Signature generation
with the Merkle Signature Scheme, the message is signed with a one-time signature scheme, resulting in a signature 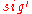, first. This is done, by using one of the public and private key pairs 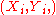.The corresponding leaf of the hash tree to a one-time public key
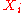is 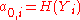. We call the path in the hash tree from to the root . The path consists of nodes, , with 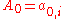being the leaf and 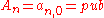being the root of the tree. To compute this path , we need every child of the nodes . We know that 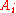is a child of . To calculate the next node of the path , we need to know both children of . So we need the brother node of . We call this node , so that 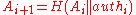. Hence, nodes 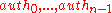are needed, to compute every node of the path . We now calculate and save these nodes 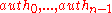.These nodes, plus the one-time signature
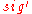of is the signature of the Merkle Signature Scheme. An example of an authentication path is illustrated in the figure on the right.Signature verification
The receiver knows the public key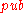, the message , and the signature . At first, the receiver verifies the one-time signature 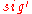of the message . If 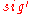is a valid signature of , the receiver computes 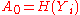by hashing the public key of the one-time signature. For , the nodes of 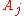of the path are computed with . If 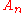equals the public key 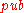of the merkle signature scheme, the signature is valid.External links
- Efficient Use of Merkle Trees - RSA labsRSA SecurityRSA, the security division of EMC Corporation, is headquartered in Bedford, Massachusetts, United States, and maintains offices in Australia, Ireland, Israel, the United Kingdom, Singapore, India, China, Hong Kong and Japan....
explanation of the original purpose of Merkle trees + Lamport signatures, as an efficient one-time signature scheme.