Mean squared prediction error
Encyclopedia
In statistics
the mean squared prediction error of a smoothing
procedure is the expected sum of squared deviations of the fitted values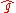
from the (unobservable) function 
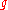. If the smoothing procedure has operator matrix 
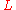, then
The MSPE can be decomposed into two terms just like mean squared error
is decomposed into bias and variance; however for MSPE one term is the sum of squared biases of the fitted values and another the sum of variances of the fitted values:
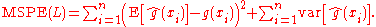
Note that knowledge of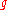
is required in order to calculate MSPE exactly.
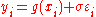where 
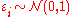, one may write
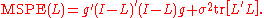
The first term is equivalent to
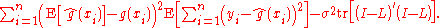
Thus,
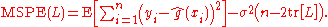
If
is known or well-estimated by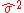 
, it becomes possible to estimate MSPE by
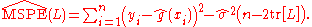
Colin Mallows advocated this method in the construction of his model selection statistic Cp
, which is a normalized version of the estimated MSPE:
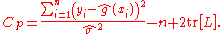
where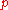
comes from that fact that the number of parameters 
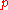estimated for a parametric smoother is given by 
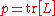, and 
is in honor of Cuthbert Daniel.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
the mean squared prediction error of a smoothing
Smoothing
In statistics and image processing, to smooth a data set is to create an approximating function that attempts to capture important patterns in the data, while leaving out noise or other fine-scale structures/rapid phenomena. Many different algorithms are used in smoothing...
procedure is the expected sum of squared deviations of the fitted values
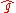from the (unobservable) function 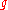. If the smoothing procedure has operator matrix 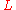, thenThe MSPE can be decomposed into two terms just like mean squared error
Mean squared error
In statistics, the mean squared error of an estimator is one of many ways to quantify the difference between values implied by a kernel density estimator and the true values of the quantity being estimated. MSE is a risk function, corresponding to the expected value of the squared error loss or...
is decomposed into bias and variance; however for MSPE one term is the sum of squared biases of the fitted values and another the sum of variances of the fitted values:
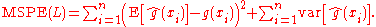
Note that knowledge of
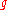is required in order to calculate MSPE exactly.Estimation of MSPE
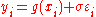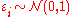For the model where , one may write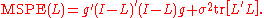The first term is equivalent to
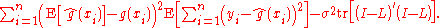
Thus,
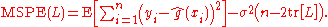
If
is known or well-estimated by 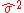, it becomes possible to estimate MSPE by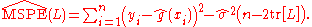Colin Mallows advocated this method in the construction of his model selection statistic Cp
Mallows' Cp
In statistics, Mallows' Cp, named for Colin L. Mallows, is used to assess the fit of a regression model that has been estimated using ordinary least squares. It is applied in the context of model selection, where a number of predictor variables are available for predicting some outcome, and the...
, which is a normalized version of the estimated MSPE:
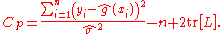
where
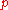comes from that fact that the number of parameters 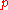estimated for a parametric smoother is given by 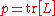, and is in honor of Cuthbert Daniel.See also
- Mean squared errorMean squared errorIn statistics, the mean squared error of an estimator is one of many ways to quantify the difference between values implied by a kernel density estimator and the true values of the quantity being estimated. MSE is a risk function, corresponding to the expected value of the squared error loss or...
- Errors and residuals in statisticsErrors and residuals in statisticsIn statistics and optimization, statistical errors and residuals are two closely related and easily confused measures of the deviation of a sample from its "theoretical value"...
- Law of total varianceLaw of total varianceIn probability theory, the law of total variance or variance decomposition formula states that if X and Y are random variables on the same probability space, and the variance of Y is finite, then...