
McCullagh's parametrization of the Cauchy distributions
Encyclopedia
In probability theory
, the "standard" Cauchy distribution
is the probability distribution
whose probability density function
is
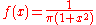
for x real
. This has median
0, and first and third quartiles respectively −1 and +1. Generally, a Cauchy distribution is any probability distribution belonging to the same location-scale family
as this one. Thus, if X has a standard Cauchy distribution and μ is any real number and σ > 0, then Y = μ + σX has a Cauchy distribution whose median is μ and whose first and third quartiles are respectively μ − σ and μ + σ.
McCullagh's parametrization, introduced by Peter McCullagh
, professor of statistics
at the University of Chicago
uses the two parameters of the non-standardised distribution to form a single complex-valued parameter, specifically, the complex number
θ = μ + iσ, where i is the imaginary unit
. It also extends the usual range of scale parameter to include σ < 0.
Although the parameter is notionally expressed using a complex number, the density is still a density over the real line. In particular the density can be written using the real-valued parameters μ and σ, which can each take positive or negative values, as
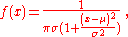
where the distribution is regarded as degenerate if σ = 0.
An alternative form for the density can be written using the complex parameter θ = μ + iσ as
where
To the question "Why introduce complex numbers when only real-valued random variable
s are involved?", McCullagh wrote:
In other words, if the random variable Y has a Cauchy distribution with complex parameter θ, then the random variable Y * defined above has a Cauchy distribution with parameter (aθ + b)/(cθ + d).
McCullagh also wrote, "The distribution of the first exit point from the upper half-plane of a Brownian particle
starting at θ is the Cauchy density on the real line with parameter θ." In addition, McCullagh shows that the complex-valued parameterisation allows a simple relationship to be made between the Cauchy and the "circular Cauchy distribution".
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, the "standard" Cauchy distribution
Cauchy distribution
The Cauchy–Lorentz distribution, named after Augustin Cauchy and Hendrik Lorentz, is a continuous probability distribution. As a probability distribution, it is known as the Cauchy distribution, while among physicists, it is known as the Lorentz distribution, Lorentz function, or Breit–Wigner...
is the probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
whose probability density function
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
is
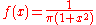
for x real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
. This has median
Median
In probability theory and statistics, a median is described as the numerical value separating the higher half of a sample, a population, or a probability distribution, from the lower half. The median of a finite list of numbers can be found by arranging all the observations from lowest value to...
0, and first and third quartiles respectively −1 and +1. Generally, a Cauchy distribution is any probability distribution belonging to the same location-scale family
Location-scale family
In probability theory, especially as that field is used in statistics, a location-scale family is a family of univariate probability distributions parametrized by a location parameter and a non-negative scale parameter; if X is any random variable whose probability distribution belongs to such a...
as this one. Thus, if X has a standard Cauchy distribution and μ is any real number and σ > 0, then Y = μ + σX has a Cauchy distribution whose median is μ and whose first and third quartiles are respectively μ − σ and μ + σ.
McCullagh's parametrization, introduced by Peter McCullagh
Peter McCullagh
Peter McCullagh is an Irish statistician, originally from Plumbridge, Northern Ireland. He attended Birmingham University and completed his Ph.D. at Imperial College London under Sir David Cox and Anthony Atkinson. He is currently the John D...
, professor of statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
at the University of Chicago
University of Chicago
The University of Chicago is a private research university in Chicago, Illinois, USA. It was founded by the American Baptist Education Society with a donation from oil magnate and philanthropist John D. Rockefeller and incorporated in 1890...
uses the two parameters of the non-standardised distribution to form a single complex-valued parameter, specifically, the complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
θ = μ + iσ, where i is the imaginary unit
Imaginary number
An imaginary number is any number whose square is a real number less than zero. When any real number is squared, the result is never negative, but the square of an imaginary number is always negative...
. It also extends the usual range of scale parameter to include σ < 0.
Although the parameter is notionally expressed using a complex number, the density is still a density over the real line. In particular the density can be written using the real-valued parameters μ and σ, which can each take positive or negative values, as
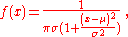
where the distribution is regarded as degenerate if σ = 0.
An alternative form for the density can be written using the complex parameter θ = μ + iσ as

where

To the question "Why introduce complex numbers when only real-valued random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s are involved?", McCullagh wrote:
In other words, if the random variable Y has a Cauchy distribution with complex parameter θ, then the random variable Y * defined above has a Cauchy distribution with parameter (aθ + b)/(cθ + d).
McCullagh also wrote, "The distribution of the first exit point from the upper half-plane of a Brownian particle
Wiener process
In mathematics, the Wiener process is a continuous-time stochastic process named in honor of Norbert Wiener. It is often called standard Brownian motion, after Robert Brown...
starting at θ is the Cauchy density on the real line with parameter θ." In addition, McCullagh shows that the complex-valued parameterisation allows a simple relationship to be made between the Cauchy and the "circular Cauchy distribution".

