
Maximum coverage problem
Encyclopedia
The maximum coverage problem is a classical question in computer science
and computational complexity theory
.
It is a problem that is widely taught in approximation algorithms.
As input you are given several sets and a number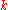 .
.
The sets may have some elements in common.
You must select at most of these sets such that the maximum number of elements are covered,
of these sets such that the maximum number of elements are covered,
i.e. the union of the selected sets has maximal size.
Formally, (unweighted) Maximum Coverage
The maximum coverage problem is NP-hard
, and cannot be approximated within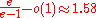 under standard assumptions.
under standard assumptions.
This result essentially matches the approximation ratio achieved by the greedy algorithm.
for maximum coverage chooses sets according to one rule: at each stage, choose a set which contains the largest number of uncovered elements. It can be shown that this algorithm achieves an approximation ratio of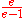 .
.
Inapproximability results show that the greedy algorithm is essentially the best-possible polynomial time approximation
algorithm for maximum coverage.
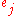 has a weight
has a weight  . The task is to find a maximum coverage which has maximum weight. The basic version is a special case when all weights are
. The task is to find a maximum coverage which has maximum weight. The basic version is a special case when all weights are 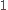 .
.
The greedy algorithm for the weighted maximum coverage at each stage chooses a set which contains the maximum weight of uncovered elements. This algorithm achieves an approximation ratio of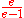 .
.
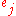 have a weight
have a weight 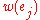 , but also every set
, but also every set 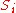 has a cost
has a cost 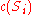 . Instead of
. Instead of 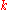 that limits the number of sets in the cover a budget
that limits the number of sets in the cover a budget  is given. This budget
is given. This budget  limits the weight of the cover that can be chosen.
limits the weight of the cover that can be chosen.
A greedy algorithm will no longer produce solutions with a performance guarantee. Namely, the worst case behavior of this algorithm might be very far from the optimal solution. The approximation algorithm is extended by the following way. First, after finding a solution using the greedy algorithm, return the better of the greedy algorithm's solution and the set of largest weight. Call this algorithm the modified greedy algorithm. Second, starting with all possible families of sets of sizes from one to (at least) three, augment these solutions with the modified greedy algorithm. Third, return the best out of all augmented solutions. This algorithm achieves an approximation ratio of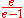 . This is the best possible approximation ratio unless
. This is the best possible approximation ratio unless 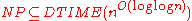 .
.
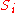 has a cost
has a cost 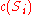 ,
,
element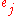 has a different weight and cost depending on which set covers it.
has a different weight and cost depending on which set covers it.
Namely, if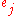 is covered by set
is covered by set 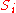 the weight of
the weight of 
is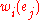 and its cost is
and its cost is 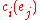 .
.
A budget is given for the total cost of the solution.
is given for the total cost of the solution.
The algorithm has several stages. First, find a solution using greedy algorithm. In each iteration of the greedy algorithm the tentative solution is added the set which contains the maximum residual weight of elements divided by the residual cost of these elements along with the residual cost of the set. Second, compare the solution gained by the first step to the best solution which uses a small number of sets. Third, return the best out of all examined solutions. This algorithm achieves an approximation ratio of .
.
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
and computational complexity theory
Computational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
.
It is a problem that is widely taught in approximation algorithms.
As input you are given several sets and a number
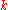 .
.The sets may have some elements in common.
You must select at most
 of these sets such that the maximum number of elements are covered,
of these sets such that the maximum number of elements are covered,i.e. the union of the selected sets has maximal size.
Formally, (unweighted) Maximum Coverage
- Instance: A number
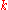 and a collection of sets
and a collection of sets  , where
, where 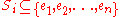 .
. - Objective: Find a subset
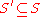 of sets, such that
of sets, such that 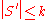 and the number of covered elements
and the number of covered elements  is maximized.
is maximized.
The maximum coverage problem is NP-hard
NP-hard
NP-hard , in computational complexity theory, is a class of problems that are, informally, "at least as hard as the hardest problems in NP". A problem H is NP-hard if and only if there is an NP-complete problem L that is polynomial time Turing-reducible to H...
, and cannot be approximated within
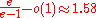 under standard assumptions.
under standard assumptions.This result essentially matches the approximation ratio achieved by the greedy algorithm.
ILP formulation
The maximum coverage problem can be formulated as the following integer linear program.- maximize
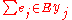 . (maximizing the sum of covered elements).
. (maximizing the sum of covered elements). - subject to
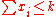 ; (no more than
; (no more than 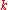 sets are selected).
sets are selected).
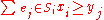 ; (if
; (if  then at least one set
then at least one set 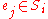 is selected).
is selected).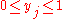 ; (if
; (if  then
then  is covered)
is covered)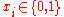 (if
(if  then
then  is selected for the cover).
is selected for the cover).
Greedy algorithm
The greedy algorithmGreedy algorithm
A greedy algorithm is any algorithm that follows the problem solving heuristic of making the locally optimal choice at each stagewith the hope of finding the global optimum....
for maximum coverage chooses sets according to one rule: at each stage, choose a set which contains the largest number of uncovered elements. It can be shown that this algorithm achieves an approximation ratio of
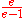 .
.Inapproximability results show that the greedy algorithm is essentially the best-possible polynomial time approximation
algorithm for maximum coverage.
Known extensions
The inapproximability results apply to all extension all maximum coverage since they hold maximum coverage as a special case.Weighted version
In the weighted version every element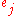 has a weight
has a weight  . The task is to find a maximum coverage which has maximum weight. The basic version is a special case when all weights are
. The task is to find a maximum coverage which has maximum weight. The basic version is a special case when all weights are 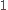 .
.- maximize
 . (maximizing the weighted sum of covered elements).
. (maximizing the weighted sum of covered elements). - subject to
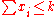 ; (no more than
; (no more than  sets are selected).
sets are selected).
 ; (if
; (if  then at least one set
then at least one set  is selected).
is selected). ; (if
; (if 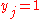 then
then 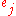 is covered)
is covered)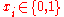 (if
(if  then
then  is selected for the cover).
is selected for the cover).
The greedy algorithm for the weighted maximum coverage at each stage chooses a set which contains the maximum weight of uncovered elements. This algorithm achieves an approximation ratio of
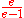 .
.Budgeted maximum coverage
In the budgeted maximum coverage version, not only does every element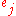 have a weight
have a weight 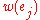 , but also every set
, but also every set 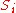 has a cost
has a cost 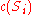 . Instead of
. Instead of 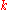 that limits the number of sets in the cover a budget
that limits the number of sets in the cover a budget  is given. This budget
is given. This budget  limits the weight of the cover that can be chosen.
limits the weight of the cover that can be chosen.- maximize
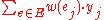 . (maximizing the weighted sum of covered elements).
. (maximizing the weighted sum of covered elements). - subject to
 ; (the cost of the selected sets cannot exceed
; (the cost of the selected sets cannot exceed  ).
).
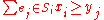 ; (if
; (if  then at least one set
then at least one set 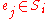 is selected).
is selected).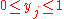 ; (if
; (if 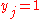 then
then 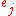 is covered)
is covered)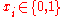 (if
(if  then
then 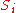 is selected for the cover).
is selected for the cover).
A greedy algorithm will no longer produce solutions with a performance guarantee. Namely, the worst case behavior of this algorithm might be very far from the optimal solution. The approximation algorithm is extended by the following way. First, after finding a solution using the greedy algorithm, return the better of the greedy algorithm's solution and the set of largest weight. Call this algorithm the modified greedy algorithm. Second, starting with all possible families of sets of sizes from one to (at least) three, augment these solutions with the modified greedy algorithm. Third, return the best out of all augmented solutions. This algorithm achieves an approximation ratio of
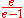 . This is the best possible approximation ratio unless
. This is the best possible approximation ratio unless 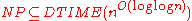 .
.Generalized maximum coverage
In the generalized maximum coverage version every set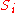 has a cost
has a cost 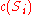 ,
,element
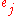 has a different weight and cost depending on which set covers it.
has a different weight and cost depending on which set covers it.Namely, if
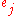 is covered by set
is covered by set 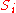 the weight of
the weight of 
is
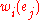 and its cost is
and its cost is 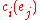 .
.A budget
 is given for the total cost of the solution.
is given for the total cost of the solution.- maximize
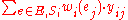 . (maximizing the weighted sum of covered elements in the sets in which they are covered).
. (maximizing the weighted sum of covered elements in the sets in which they are covered). - subject to
 ; (the cost of the selected sets cannot exceed
; (the cost of the selected sets cannot exceed  ).
).
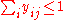 ; (element
; (element 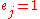 can only be covered by at most one set).
can only be covered by at most one set). ; (if
; (if  then at least one set
then at least one set  is selected).
is selected).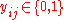 ; (if
; (if 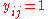 then
then 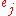 is covered by set
is covered by set 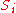 )
)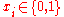 (if
(if  then
then 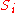 is selected for the cover).
is selected for the cover).
Generalized maximum coverage algorithm
The algorithm uses the concept of residual cost/weight. The residual cost/weight is measured against a tentative solution and its the difference of the cost/weight from the cost/weight gained by a tentative solution.The algorithm has several stages. First, find a solution using greedy algorithm. In each iteration of the greedy algorithm the tentative solution is added the set which contains the maximum residual weight of elements divided by the residual cost of these elements along with the residual cost of the set. Second, compare the solution gained by the first step to the best solution which uses a small number of sets. Third, return the best out of all examined solutions. This algorithm achieves an approximation ratio of
 .
.Related problems
- Set cover problemSet cover problemThe set covering problem is a classical question in computer science and complexity theory.It is a problem "whose study has led to the development of fundamental techniques for the entire field" of approximation algorithms...
is to cover all elements with as few sets as possible.

