
Maximal arc
Encyclopedia
Maximal arcs are  -arcs
-arcs
in a projective plane, where k is maximal with respect to the parameter d and the ambient space.
 be a projective plane of order q (not necessarily desarguesian). Maximal arcs of degree d (
be a projective plane of order q (not necessarily desarguesian). Maximal arcs of degree d ( )are
)are 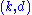 -arcs
-arcs
in , where k is maximal with respect to the parameter d or thus
, where k is maximal with respect to the parameter d or thus 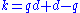 .
.
Equivalently, one can define maximal arcs of degree d in as a set of points K(
as a set of points K(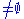 ) such that every line intersect it either in 0 or d points.
) such that every line intersect it either in 0 or d points.
, derived from maximal arcs
 -arcs
-arcsArc (projective geometry)
In mathematics, a -arc in a finite projective plane π is a set of k points of \pi such that each line intersects A in at most d points, and there is at least one line that does intersect A in d points...
in a projective plane, where k is maximal with respect to the parameter d and the ambient space.
Definition
Let be a projective plane of order q (not necessarily desarguesian). Maximal arcs of degree d (
be a projective plane of order q (not necessarily desarguesian). Maximal arcs of degree d ( )are
)are 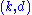 -arcs
-arcsArc (projective geometry)
In mathematics, a -arc in a finite projective plane π is a set of k points of \pi such that each line intersects A in at most d points, and there is at least one line that does intersect A in d points...
in
 , where k is maximal with respect to the parameter d or thus
, where k is maximal with respect to the parameter d or thus 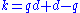 .
.Equivalently, one can define maximal arcs of degree d in
 as a set of points K(
as a set of points K(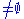 ) such that every line intersect it either in 0 or d points.
) such that every line intersect it either in 0 or d points.Properties
-
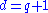 occurs if and only if every point is in K.
occurs if and only if every point is in K. - The number of lines through a fixed point p, not on K (provided that
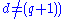 , intersecting K in one point, equals
, intersecting K in one point, equals 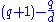 . Thus if
. Thus if  , d divides q
, d divides q -
 occurs if and only if K contains exactly one point.
occurs if and only if K contains exactly one point. -
 occurs if and only if K contains all points except the points on a fixed line.
occurs if and only if K contains all points except the points on a fixed line. - In
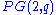 with q odd, no maximal arcs of degree d with
with q odd, no maximal arcs of degree d with 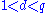 exist.
exist. - In
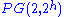 , maximal arcs for every degree
, maximal arcs for every degree 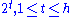 exist.
exist.
Partial geometries
One can construct partial geometriesPartial geometry
An incidence structure C= consists of points P, lines L, and flags I \subseteq P \times L where a point p is said to be incident with a line l if \in I...
, derived from maximal arcs
- Let K be a maximal arc with degree
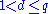 . Consider the incidence structure
. Consider the incidence structure  , where P contains all points of the projective plane not on K, B contains all line of the projective plane intersecting K in d points, and the incidence I is the natural inclusion. This is a partial geometry :
, where P contains all points of the projective plane not on K, B contains all line of the projective plane intersecting K in d points, and the incidence I is the natural inclusion. This is a partial geometry :  .
. - Consider the space
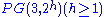 and let K a maximal arc of degree
and let K a maximal arc of degree 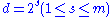 in a two-dimensional subspace
in a two-dimensional subspace  . Consider an incidence structure
. Consider an incidence structure 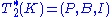 where P contains all the points not in
where P contains all the points not in  , B contains all lines not in
, B contains all lines not in  and intersecting
and intersecting  in a point in K, and I is again the natural inclusion.
in a point in K, and I is again the natural inclusion.  is again a partial geometry :
is again a partial geometry :  .
.

