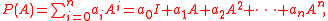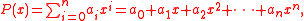Matrix polynomial
Encyclopedia
In mathematics, a matrix polynomial is a polynomial with matrices
as variables. Examples include:
A matrix polynomial equation is an equality between two matrix polynomials, which holds for the specific matrices in question. If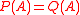 , (where A is a matrix over a field), then the eigenvalues of A satisfy the characteristic equation
, (where A is a matrix over a field), then the eigenvalues of A satisfy the characteristic equation 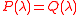 .
.
A matrix polynomial identity is a matrix polynomial equation which holds for all matricies A in a specified matrix ring
Mn(R).
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
as variables. Examples include:
-
- where P is a polynomial,
-
- and I is the identity matrix.
-
- the commutator of A and B.
A matrix polynomial equation is an equality between two matrix polynomials, which holds for the specific matrices in question. If
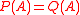 , (where A is a matrix over a field), then the eigenvalues of A satisfy the characteristic equation
, (where A is a matrix over a field), then the eigenvalues of A satisfy the characteristic equation 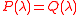 .
.A matrix polynomial identity is a matrix polynomial equation which holds for all matricies A in a specified matrix ring
Matrix ring
In abstract algebra, a matrix ring is any collection of matrices forming a ring under matrix addition and matrix multiplication. The set of n×n matrices with entries from another ring is a matrix ring, as well as some subsets of infinite matrices which form infinite matrix rings...
Mn(R).