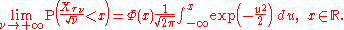Martingale central limit theorem
Encyclopedia
In probability theory
, the central limit theorem
says that, under certain conditions, the sum of many independent identically-distributed random variables, when scaled appropriately, converges in distribution to a standard normal distribution. The martingale central limit theorem generalizes this result for random variables to martingale
s, which are stochastic process
es where the change in the value of the process from time t to time t + 1 has expectation
zero, even conditioned on previous outcomes.
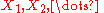 -- be a martingale with bounded increments, i.e., suppose
-- be a martingale with bounded increments, i.e., suppose
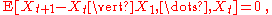
and
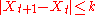
almost surely
for some fixed bound k and all t. Also assume that almost surely.
almost surely.
Define
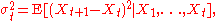
and let

Then
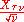
converges in distribution to the normal distribution with mean 0 and variance 1 as . More explicitly,
. More explicitly,
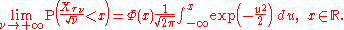
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, the central limit theorem
Central limit theorem
In probability theory, the central limit theorem states conditions under which the mean of a sufficiently large number of independent random variables, each with finite mean and variance, will be approximately normally distributed. The central limit theorem has a number of variants. In its common...
says that, under certain conditions, the sum of many independent identically-distributed random variables, when scaled appropriately, converges in distribution to a standard normal distribution. The martingale central limit theorem generalizes this result for random variables to martingale
Martingale (probability theory)
In probability theory, a martingale is a model of a fair game where no knowledge of past events can help to predict future winnings. In particular, a martingale is a sequence of random variables for which, at a particular time in the realized sequence, the expectation of the next value in the...
s, which are stochastic process
Stochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
es where the change in the value of the process from time t to time t + 1 has expectation
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
zero, even conditioned on previous outcomes.
Statement
Here is a simple version of the martingale central limit theorem: Let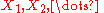 -- be a martingale with bounded increments, i.e., suppose
-- be a martingale with bounded increments, i.e., suppose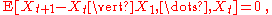
and
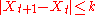
almost surely
Almost surely
In probability theory, one says that an event happens almost surely if it happens with probability one. The concept is analogous to the concept of "almost everywhere" in measure theory...
for some fixed bound k and all t. Also assume that
 almost surely.
almost surely.Define
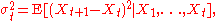
and let

Then
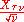
converges in distribution to the normal distribution with mean 0 and variance 1 as
 . More explicitly,
. More explicitly,