Markov kernel
Encyclopedia
In probability theory
, a Markov kernel is a map that plays the role, in the general theory of Markov process
es, that the transition matrix does in the theory of Markov processes with a finite state space.
, 
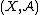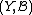be measurable spaces. A Markov kernel with source 
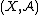and target 
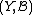is a map 
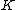that associates to each point 
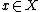a probability measure
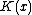on 
such that, for every measurable set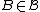 
, the map 
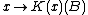is measurable with respect to the 
-algebra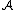 
.
Let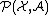
denote the set of all probability measures on the measurable
space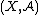
. If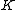 
is a Markov kernel with source 
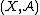and target 
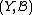then we can naturally associate to 
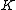a map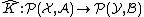 
defined as follows: given 
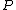in 
, we set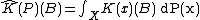 
, for all 
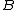in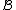 
.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, a Markov kernel is a map that plays the role, in the general theory of Markov process
Markov process
In probability theory and statistics, a Markov process, named after the Russian mathematician Andrey Markov, is a time-varying random phenomenon for which a specific property holds...
es, that the transition matrix does in the theory of Markov processes with a finite state space.
Formal definition
Let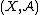, 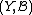be measurable spaces. A Markov kernel with source 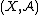and target 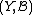is a map 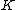that associates to each point 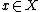a probability measureProbability measure
In mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as countable additivity...
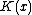on such that, for every measurable set 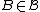, the map 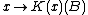is measurable with respect to the -algebra 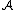.Let
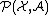denote the set of all probability measures on the measurablespace
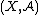. If 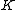is a Markov kernel with source 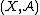and target 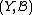then we can naturally associate to 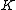a map 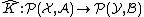defined as follows: give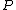n in , we set 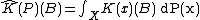, for all 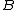in 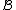.