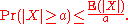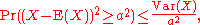Markov's inequality - AbsoluteAstronomy.com

Probability theory

Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...

, Markov's inequality gives an upper bound

Upper bound

In mathematics, especially in order theory, an upper bound of a subset S of some partially ordered set is an element of P which is greater than or equal to every element of S. The term lower bound is defined dually as an element of P which is lesser than or equal to every element of S...

for the probability

Probability

Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...

that a non-negative function

Function (mathematics)

In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...

of a random variable

Random variable

In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...

is greater than or equal to some positive constant

Constant (mathematics)

In mathematics, a constant is a non-varying value, i.e. completely fixed or fixed in the context of use. The term usually occurs in opposition to variable In mathematics, a constant is a non-varying value, i.e. completely fixed or fixed in the context of use. The term usually occurs in opposition...

. It is named after the Russian mathematician Andrey Markov

Andrey Markov

Andrey Andreyevich Markov was a Russian mathematician. He is best known for his work on theory of stochastic processes...

, although it appeared earlier in the work of Pafnuty Chebyshev

Pafnuty Chebyshev

Pafnuty Lvovich Chebyshev was a Russian mathematician. His name can be alternatively transliterated as Chebychev, Chebysheff, Chebyshov, Tschebyshev, Tchebycheff, or Tschebyscheff .-Early years:One of nine children, Chebyshev was born in the village of Okatovo in the district of Borovsk,...

(Markov's teacher), and many sources, especially in analysis

Mathematical analysis

Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...

, refer to it as Chebyshev's inequality

Chebyshev's inequality

In probability theory, Chebyshev’s inequality guarantees that in any data sample or probability distribution,"nearly all" values are close to the mean — the precise statement being that no more than 1/k2 of the distribution’s values can be more than k standard deviations away from the mean...

or Bienaymé

Irénée-Jules Bienaymé

Irénée-Jules Bienaymé , was a French statistician. He built on the legacy of Laplace generalizing his least squares method. He contributed to the fields and probability, and statistics and to their application to finance, demography and social sciences...

's inequality.

Markov's inequality (and other similar inequalities) relate probabilities to expectation

Expected value

In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...

s, and provide (frequently) loose but still useful bounds for the cumulative distribution function

Cumulative distribution function

In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...

of a random variable.

An example of an application of Markov's inequality is the fact that (assuming incomes are non-negative) no more than 1/5 of the population can have more than 5 times the average income.

Statement

If X is any random variable and a > 0, then

In the language of measure theory, Markov's inequality states that if (X, Σ, μ) is a measure space

Measure (mathematics)

In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...

, ƒ is a measurable

Measurable function

In mathematics, particularly in measure theory, measurable functions are structure-preserving functions between measurable spaces; as such, they form a natural context for the theory of integration...

extended real

Extended real number line

In mathematics, the affinely extended real number system is obtained from the real number system R by adding two elements: +∞ and −∞ . The projective extended real number system adds a single object, ∞ and makes no distinction between "positive" or "negative" infinity...

-valued function, and

, then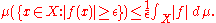

Corollary: Chebyshev's inequality

Chebyshev's inequality

uses the variance to bound the probability that a random variable deviates far from the mean. Specifically:

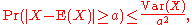
for any a>0. Here Var(X) is the variance of X, defined as:

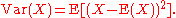
Chebyshev's inequality follows from Markov's inequality by considering the random variable

for which Markov's inequality reads

Proofs

We separate the case in which the measure space is a probability space from the more general case because the probability case is more accessible for the general reader.

In the language of probability theory

For any event E, let I_E be the indicator random variable of E, that is, I_E = 1 if E occurs and = 0 otherwise. Thus I_{(|X| ≥ a)} = 1 if the event |X| ≥ a occurs, and I_{(|X| ≥ a)} = 0 if |X| < a. Then, given a > 0,

which is clear if we consider the two possible values of I_{(|X| ≥ a)}. Either |X| < a and thus I_{(|X| ≥ a)} = 0, or I_{(|X| ≥ a)} = 1 and by the condition of I_{(|X| ≥ a)}, the inequality must be true.

Therefore

Now, using linearity of expectations, the left side of this inequality is the same as

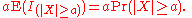
Thus we have

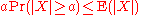
and since a > 0, we can divide both sides by a.

In the language of measure theory

We may assume that the function

is non-negative, since only its absolute value enters in the equation. Now, consider the real-valued function s on X given by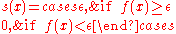

Then

is a simple function such that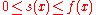

. By the definition of the Lebesgue integral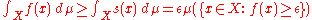

and since

, both sides can be divided by

, obtaining

Q.E.D.

Q.E.D. is an initialism of the Latin phrase , which translates as "which was to be demonstrated". The phrase is traditionally placed in its abbreviated form at the end of a mathematical proof or philosophical argument when what was specified in the enunciation — and in the setting-out —...

Statement

Corollary: Chebyshev's inequality

Proofs

In the language of probability theory

In the language of measure theory

See also