
Malcev algebra
Encyclopedia
In mathematics
, a Malcev algebra (or Maltsev algebra or Moufang
–Lie
algebra) over a field is a nonassociative algebra that is antisymmetric, so that
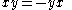
and satisfies the Malcev identity
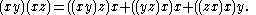
They were first defined by Anatoly Maltsev
(1955).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Malcev algebra (or Maltsev algebra or Moufang
Ruth Moufang
Ruth Moufang was a German mathematician.Born to a German chemist Dr. Eduard Moufang and Else Fecht Moufang, she studied mathematics at the University of Frankfurt. In 1931 she received her Ph.D. on projective geometry under the direction of Max Dehn, and in 1932 spent a fellowship year in Rome...
–Lie
Sophus Lie
Marius Sophus Lie was a Norwegian mathematician. He largely created the theory of continuous symmetry, and applied it to the study of geometry and differential equations.- Biography :...
algebra) over a field is a nonassociative algebra that is antisymmetric, so that
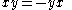
and satisfies the Malcev identity
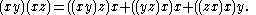
They were first defined by Anatoly Maltsev
Anatoly Maltsev
Anatoly Ivanovich Maltsev was born in Misheronsky, near Moscow, and died in Novosibirsk, USSR. He was a mathematician noted for his work on the decidability of various algebraic groups...
(1955).
Examples
- Any Lie algebraLie algebraIn mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
is a Malcev algebra. - Any alternative algebraAlternative algebraIn abstract algebra, an alternative algebra is an algebra in which multiplication need not be associative, only alternative. That is, one must have*x = y*x = y...
may be made into a Malcev algebra by defining the Malcev product to be xy − yx. - The imaginary octonions form a 7-dimensional Malcev algebra by defining the Malcev product to be xy − yx.

