Maier's theorem
Encyclopedia
In number theory, Maier's theorem is a theorem about the numbers of prime
s in short intervals for which the Cramér's probabilistic model of primes gives the wrong answer.
It states that if π is the prime counting function
and λ is greater than 1 then
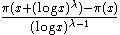
does not have a limit as x tends to infinity; more precisely the lim sup is greater than 1, and the lim inf is less than 1. The Cramér's probabilistic model of primes predicts incorrectly that it has limit 1 when λ≥2 (using the Borel–Cantelli lemma).
Maier's theorem uses the beautiful Buchstab's equivalent for the counting function of quasi-primes (set of numbers without prime factors lower to bound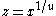
, 
fixed). It also uses an equivalent of the number of primes in arithmetic progressions of sufficient length due to Gallagher.
gave another proof, and also showed that most probabilistic models of primes incorrectly predict the mean square error
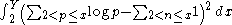
of one version of the prime number theorem
.
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s in short intervals for which the Cramér's probabilistic model of primes gives the wrong answer.
It states that if π is the prime counting function
Prime counting function
In mathematics, the prime-counting function is the function counting the number of prime numbers less than or equal to some real number x. It is denoted by \scriptstyle\pi .-History:...
and λ is greater than 1 then
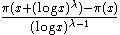
does not have a limit as x tends to infinity; more precisely the lim sup is greater than 1, and the lim inf is less than 1. The Cramér's probabilistic model of primes predicts incorrectly that it has limit 1 when λ≥2 (using the Borel–Cantelli lemma).
Maier's theorem uses the beautiful Buchstab's equivalent for the counting function of quasi-primes (set of numbers without prime factors lower to bound
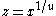, fixed). It also uses an equivalent of the number of primes in arithmetic progressions of sufficient length due to Gallagher.gave another proof, and also showed that most probabilistic models of primes incorrectly predict the mean square error
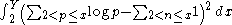
of one version of the prime number theorem
Prime number theorem
In number theory, the prime number theorem describes the asymptotic distribution of the prime numbers. The prime number theorem gives a general description of how the primes are distributed amongst the positive integers....
.