
Machin-like formula
Encyclopedia
In mathematics
, Machin-like formulae are a class of identities involving π
= 3.14159... that generalize John Machin
's formula from 1706:
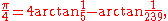
which he used along with the Taylor series
arctangent expansion to compute π to 100 decimal places.
Machin-like formulas have the form

with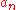 and
and 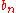 integer
integer
s.
The same method is still among the most efficient known for computing a large number of digits of π with digital computer
s.
In other words, for small numbers, arctangent is to a good approximation just the identity function. This leads to the possibility that a number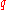 can be found such that
can be found such that
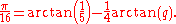
Using elementary algebra, we can isolate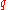 :
:

Using the identities above, we substitute arctan(1) for π/4 and then expand the result.

Similarly, two applications of the double angle identity yields

and so
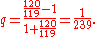
Other formulas may be generated using complex numbers. For example the angle of a complex number a+bi is given by and when you multiply complex numbers you add their angles. If a=b then
and when you multiply complex numbers you add their angles. If a=b then  is 45 degrees or
is 45 degrees or 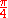 . This means that if the real part and complex part are equal then the arctangent will equal
. This means that if the real part and complex part are equal then the arctangent will equal 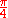 . Since the arctangent of one has a very slow convergence rate if we find two complex numbers that when multiplied will result in the same real and imaginary part we will have a Machin-like formula. An example is
. Since the arctangent of one has a very slow convergence rate if we find two complex numbers that when multiplied will result in the same real and imaginary part we will have a Machin-like formula. An example is  and
and  . If we multiply these out we will get
. If we multiply these out we will get  . Therefore
. Therefore  .
.
If you want to use complex numbers to show that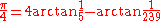 you first must know that when multiplying angles you put the complex number to the power of the number that you are multiplying by. So
you first must know that when multiplying angles you put the complex number to the power of the number that you are multiplying by. So  and since the real part and imaginary part are equal then,
and since the real part and imaginary part are equal then, 
's
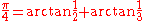 ,
,
Hermann's,
 ,
,
and Hutton's
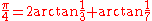 .
.
of Tokyo University. A 64-node Hitachi
supercomputer
with 1 terabyte of main memory, performing 2 trillion operations per second, was used to evaluate the following Machin-like formulas:

The more efficient currently known Machin-like formulas for computing:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Machin-like formulae are a class of identities involving π
Pi
' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
= 3.14159... that generalize John Machin
John Machin
John Machin, , a professor of astronomy at Gresham College, London, is best known for developing a quickly converging series for Pi in 1706 and using it to compute Pi to 100 decimal places.Machin's formula is:...
's formula from 1706:
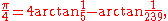
which he used along with the Taylor series
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
arctangent expansion to compute π to 100 decimal places.
Machin-like formulas have the form

with
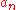 and
and 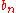 integer
integerInteger
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s.
The same method is still among the most efficient known for computing a large number of digits of π with digital computer
Computer
A computer is a programmable machine designed to sequentially and automatically carry out a sequence of arithmetic or logical operations. The particular sequence of operations can be changed readily, allowing the computer to solve more than one kind of problem...
s.
Derivation
To understand where this formula comes from, start with following basic ideas:-

-

-
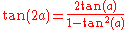 (tangent double angle identity)
(tangent double angle identity) -
 (tangent difference identity)
(tangent difference identity) -
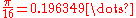 (approximately)
(approximately) -
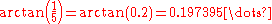 (approximately)
(approximately)
In other words, for small numbers, arctangent is to a good approximation just the identity function. This leads to the possibility that a number
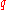 can be found such that
can be found such that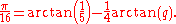
Using elementary algebra, we can isolate
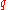 :
:
Using the identities above, we substitute arctan(1) for π/4 and then expand the result.

Similarly, two applications of the double angle identity yields

and so
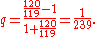
Other formulas may be generated using complex numbers. For example the angle of a complex number a+bi is given by
 and when you multiply complex numbers you add their angles. If a=b then
and when you multiply complex numbers you add their angles. If a=b then  is 45 degrees or
is 45 degrees or 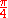 . This means that if the real part and complex part are equal then the arctangent will equal
. This means that if the real part and complex part are equal then the arctangent will equal 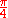 . Since the arctangent of one has a very slow convergence rate if we find two complex numbers that when multiplied will result in the same real and imaginary part we will have a Machin-like formula. An example is
. Since the arctangent of one has a very slow convergence rate if we find two complex numbers that when multiplied will result in the same real and imaginary part we will have a Machin-like formula. An example is  and
and  . If we multiply these out we will get
. If we multiply these out we will get  . Therefore
. Therefore  .
.If you want to use complex numbers to show that
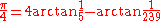 you first must know that when multiplying angles you put the complex number to the power of the number that you are multiplying by. So
you first must know that when multiplying angles you put the complex number to the power of the number that you are multiplying by. So  and since the real part and imaginary part are equal then,
and since the real part and imaginary part are equal then, 
Two-term formulas
There are exactly three additional Machin-like formulas with two terms; these are EulerLeonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
's
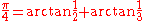 ,
,Hermann's,
 ,
,and Hutton's
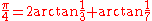 .
.More terms
The 2002 record for digits of π, 1,241,100,000,000, was obtained by Yasumasa KanadaYasumasa Kanada
is a Japanese mathematician most known for his numerous world records over the past three decades for calculating digits of π. He has set the record 11 of the past 21 times....
of Tokyo University. A 64-node Hitachi
Hitachi, Ltd.
is a Japanese multinational conglomerate headquartered in Marunouchi 1-chome, Chiyoda, Tokyo, Japan. The company is the parent of the Hitachi Group as part of the larger DKB Group companies...
supercomputer
Supercomputer
A supercomputer is a computer at the frontline of current processing capacity, particularly speed of calculation.Supercomputers are used for highly calculation-intensive tasks such as problems including quantum physics, weather forecasting, climate research, molecular modeling A supercomputer is a...
with 1 terabyte of main memory, performing 2 trillion operations per second, was used to evaluate the following Machin-like formulas:

- Kikuo TakanoKikuo Takanowas a Japanese poet and mathematician. He was born on Sado Island in 1927. He graduated from Utsunomiya Agricultural College in 1948.He began to write poems from the next day Japan had ended its role in World War II. Being inspired from surrealism and Heidegger, he wrote poems that asks the meaning...
(1982).
-
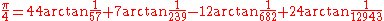
- F. C. W. StörmerCarl StørmerFredrik Carl Mülertz Størmer was a Norwegian mathematician and physicist, known both for his work in number theory and for studying the movement of charged particles in the magnetosphere and the formation of aurorae....
(1896).
The more efficient currently known Machin-like formulas for computing:
-

- 黃見利(Hwang Chien-Lih) (1997).
-
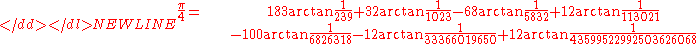
- 黃見利(Hwang Chien-Lih) (2003).
These Machin-like formula is shown by the following identities;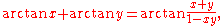

or equivalently,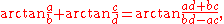
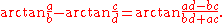
These identities are easily derived from the definition of arctangent.
With these identities, we shall show the Machin-like formula such as Takano; :
:
External links
- The constant π
- Machin's Merit at MathPages
- Archimedes' constant pi - Machin's formula gives a proof for the John Machin`s formula

