
MacLaurin's inequality
Encyclopedia
In mathematics
, Maclaurin's inequality, named after Colin Maclaurin
, is a refinement of the inequality of arithmetic and geometric means
.
Let a1, a2, ..., an be positive real number
s, and for k = 1, 2, ..., n define the averages Sk as follows:
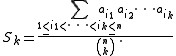
The numerator of this fraction is the elementary symmetric polynomial
of degree k in the n variables a1, a2, ..., an, that is, the sum of all products of k of the numbers a1, a2, ..., an with the indices in increasing order. The denominator is the number of terms in the numerator, the binomial coefficient

Maclaurin's inequality is the following chain of inequalities:
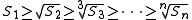
with equality if and only if all the ai are equal.
For n = 2, this gives the usual inequality of arithmetic and geometric means of two numbers. Maclaurin's inequality is well illustrated by the case n = 4:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Maclaurin's inequality, named after Colin Maclaurin
Colin Maclaurin
Colin Maclaurin was a Scottish mathematician who made important contributions to geometry and algebra. The Maclaurin series, a special case of the Taylor series, are named after him....
, is a refinement of the inequality of arithmetic and geometric means
Inequality of arithmetic and geometric means
In mathematics, the inequality of arithmetic and geometric means, or more briefly the AM–GM inequality, states that the arithmetic mean of a list of non-negative real numbers is greater than or equal to the geometric mean of the same list; and further, that the two means are equal if and only if...
.
Let a1, a2, ..., an be positive real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s, and for k = 1, 2, ..., n define the averages Sk as follows:
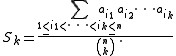
The numerator of this fraction is the elementary symmetric polynomial
Elementary symmetric polynomial
In mathematics, specifically in commutative algebra, the elementary symmetric polynomials are one type of basic building block for symmetric polynomials, in the sense that any symmetric polynomial P can be expressed as a polynomial in elementary symmetric polynomials: P can be given by an...
of degree k in the n variables a1, a2, ..., an, that is, the sum of all products of k of the numbers a1, a2, ..., an with the indices in increasing order. The denominator is the number of terms in the numerator, the binomial coefficient
Binomial coefficient
In mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...

Maclaurin's inequality is the following chain of inequalities:
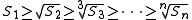
with equality if and only if all the ai are equal.
For n = 2, this gives the usual inequality of arithmetic and geometric means of two numbers. Maclaurin's inequality is well illustrated by the case n = 4:
-
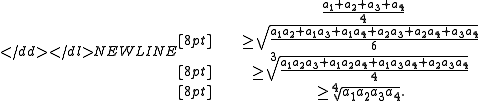
Maclaurin's inequality can be proved using the Newton's inequalitiesNewton's inequalitiesIn mathematics, the Newton inequalities are named after Isaac Newton. Suppose a1, a2, ..., an are real numbers and let \sigma_k denote the kth elementary symmetric function in a1, a2, ..., an...
.
See also
- Newton's inequalitiesNewton's inequalitiesIn mathematics, the Newton inequalities are named after Isaac Newton. Suppose a1, a2, ..., an are real numbers and let \sigma_k denote the kth elementary symmetric function in a1, a2, ..., an...
- Muirhead's inequalityMuirhead's inequalityIn mathematics, Muirhead's inequality, named after Robert Franklin Muirhead, also known as the "bunching" method, generalizes the inequality of arithmetic and geometric means.-The "a-mean":For any real vectora=...
- Generalized mean inequality
- Newton's inequalities

