
MAX-3SAT
Encyclopedia
MAX-3SAT is a problem in the computational complexity
subfield of computer science
. It generalises the Boolean satisfiability problem
(SAT) which is a decision problem
considered in complexity theory
. It is defined as:
Given a 3-CNF formula Φ (i.e. with at most 3 variables per clause), Find an assignment that satisfies the largest number of clauses.
MAX-3SAT is a canonical complete
problem for the complexity class MAXSNP (shown complete in Papadimitriou pg. 314).
. Therefore, a polynomial-time solution can only be achieved if P = NP. An approximation within a factor of 2 can be achieved with this simple algorithm, however:
The Karloff-Zwick algorithm
runs in polynomial-time and satisfies ≥ 7/8 of the clauses.
implies that there exists an ε > 0 such that (1-ε)-approximation of MAX-3SAT is NP-hard
.
Proof:
Any NP-complete
problem L ∈ PCP(O(log (n)), O(1)) by the PCP theorem
. For x ∈ L, a 3-CNF formula Ψx is constructed so that
The Verifier V reads all required bits at once i.e. makes non-adaptive queries. This is valid because the number of queries remains constant.
Next we try to find a Boolean
formula to simulate this. We introduce Boolean variables x1,...,xl, where l is the length of the proof. To demonstrate that the Verifier runs in Probabilistic polynomial-time, we need a correspondence between the number of satisfiable clauses and the probability the Verifier accepts.
It can be concluded that if this holds for every NP-complete
problem then the PCP theorem
must be true.
He constructs a PCP Verifier for 3-SAT that reads only 3 bits from the Proof.
For every ε > 0, there is a PCP-verifier M for 3-SAT that reads a random string r of length O(log(n)) and computes query positions ir, jr, kr in the proof π and a bit br. It accepts if and only if
π(ir) ⊕ π(jr) ⊕ π(kr) ⊕ = br.
The Verifier has completeness (1-ε) and soundness 1/2 + ε (refer to PCP (complexity)
). The Verifier satisfies
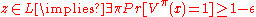
This is enough to prove the hardness of approximation ratio
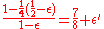
MAX-3SAT(B) is the restricted special case of MAX-3SAT where every variable occurs in at most B clauses. Before the PCP theorem
was proven, Papadimitriou and Yannakakis showed that for some fixed constant B, this problem is MAX SNP-hard. Consequently with the PCP theorem, it is also APX-hard. This is useful because MAX-3SAT(B) can often be used to obtain a PTAS-preserving reduction in a way that MAX-3SAT cannot. Proofs for explicit values of B include: all B ≥ 13, and all B ≥ 3 (which is best possible).
Moreover, although the decision problem 2SAT is solvable in polynomial time, MAX-2SAT(3) is also APX-hard.
The best possible approximation ratio for MAX-3SAT(B), as a function of B, is at least and at most
and at most 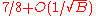 , unless NP=RP. Some explicit bounds on the approximability constants for certain values of B are known.
, unless NP=RP. Some explicit bounds on the approximability constants for certain values of B are known.
MAX-EkSAT
is a paramaterized version of MAX-3SAT where every clause has exactly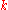 literals, for k ≥ 3. It can be efficiently approximated with approximation ratio
literals, for k ≥ 3. It can be efficiently approximated with approximation ratio 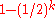 using ideas from coding theory.
using ideas from coding theory.
Computational Complexity
Computational Complexity may refer to:*Computational complexity theory*Computational Complexity...
subfield of computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
. It generalises the Boolean satisfiability problem
Boolean satisfiability problem
In computer science, satisfiability is the problem of determining if the variables of a given Boolean formula can be assigned in such a way as to make the formula evaluate to TRUE...
(SAT) which is a decision problem
Decision problem
In computability theory and computational complexity theory, a decision problem is a question in some formal system with a yes-or-no answer, depending on the values of some input parameters. For example, the problem "given two numbers x and y, does x evenly divide y?" is a decision problem...
considered in complexity theory
Computational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
. It is defined as:
Given a 3-CNF formula Φ (i.e. with at most 3 variables per clause), Find an assignment that satisfies the largest number of clauses.
MAX-3SAT is a canonical complete
Complete (complexity)
In computational complexity theory, a computational problem is complete for a complexity class if it is, in a formal sense, one of the "hardest" or "most expressive" problems in the complexity class...
problem for the complexity class MAXSNP (shown complete in Papadimitriou pg. 314).
Approximability
The decision version of MAX-3SAT is NP-completeNP-complete
In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...
. Therefore, a polynomial-time solution can only be achieved if P = NP. An approximation within a factor of 2 can be achieved with this simple algorithm, however:
- Output the solution in which most clauses are satisfied, when either all variables = TRUE or all variables = FALSE.
- Every clause is satisfied by one of the two solutions, therefore one solution satisfies at least half of the clauses.
The Karloff-Zwick algorithm
Karloff-Zwick algorithm
The Karloff–Zwick algorithm, in computational complexity theory, is a randomised approximation algorithm taking an instance of MAX-3SAT Boolean satisfiability problem as input. If the instance is satisfiable, then the expected weight of the assignment found is at least 7/8 of optimal...
runs in polynomial-time and satisfies ≥ 7/8 of the clauses.
Theorem 1 (Inapproximability)
The PCP theoremPCP theorem
In computational complexity theory, the PCP theorem states that every decision problem in the NP complexity class has probabilistically checkable proofs of constant query complexity and logarithmic randomness complexity .The PCP theorem says that for some universal constant K, for every...
implies that there exists an ε > 0 such that (1-ε)-approximation of MAX-3SAT is NP-hard
NP-hard
NP-hard , in computational complexity theory, is a class of problems that are, informally, "at least as hard as the hardest problems in NP". A problem H is NP-hard if and only if there is an NP-complete problem L that is polynomial time Turing-reducible to H...
.
Proof:
Any NP-complete
NP-complete
In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...
problem L ∈ PCP(O(log (n)), O(1)) by the PCP theorem
PCP theorem
In computational complexity theory, the PCP theorem states that every decision problem in the NP complexity class has probabilistically checkable proofs of constant query complexity and logarithmic randomness complexity .The PCP theorem says that for some universal constant K, for every...
. For x ∈ L, a 3-CNF formula Ψx is constructed so that
- x ∈ L ⇒ Ψx is satisfiable
- x ∉ L ⇒ no more than (1-ε)m clauses of Ψx are satisfiable.
The Verifier V reads all required bits at once i.e. makes non-adaptive queries. This is valid because the number of queries remains constant.
- Let q be the number of queries.
- Enumerating all random strings Ri ∈ V, we obtain poly(x) strings since the length of each string r(x) = O(log |x|).
- For each Ri
- V chooses q positions i1,...,iq and a Boolean function fR: {0,1}q->{0,1} and accepts if and only if fR(π(i1,...,iq)). Here π refers to the proof obtained from the Oracle.
Next we try to find a Boolean
Boolean logic
Boolean algebra is a logical calculus of truth values, developed by George Boole in the 1840s. It resembles the algebra of real numbers, but with the numeric operations of multiplication xy, addition x + y, and negation −x replaced by the respective logical operations of...
formula to simulate this. We introduce Boolean variables x1,...,xl, where l is the length of the proof. To demonstrate that the Verifier runs in Probabilistic polynomial-time, we need a correspondence between the number of satisfiable clauses and the probability the Verifier accepts.
- For every R, add clauses representing fR(xi1,...,xiq) using 2q SATSATThe SAT Reasoning Test is a standardized test for college admissions in the United States. The SAT is owned, published, and developed by the College Board, a nonprofit organization in the United States. It was formerly developed, published, and scored by the Educational Testing Service which still...
clauses. Clauses of length q are converted to length 3 by adding new (auxiliary) variables e.g. x2 ∨ x10 ∨ x11 ∨ x12 = ( x2 ∨ x10 ∨ yR) ∧ (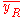 ∨ x11 ∨ x12). This requires a maximum of q2q 3-SAT clauses.
∨ x11 ∨ x12). This requires a maximum of q2q 3-SAT clauses. - If z ∈ L then
- there is a proof π such that Vπ (z) accepts for every Ri.
- All clauses are satisfied if xi = π(i) and the auxiliary variables are added correctly.
- If input z ∉ L then
- For every assignment to x1,...,xl and yR's, the corresponding proof π(i) = xi causes the Verifier to reject for half of all R ∈ {0,1}r(|z|).
- For each R, one clause representing fR fails.
- Therefore a fraction
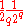 of clauses fails.
of clauses fails.
- For every assignment to x1,...,xl and yR's, the corresponding proof π(i) = xi causes the Verifier to reject for half of all R ∈ {0,1}r(|z|).
It can be concluded that if this holds for every NP-complete
NP-complete
In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...
problem then the PCP theorem
PCP theorem
In computational complexity theory, the PCP theorem states that every decision problem in the NP complexity class has probabilistically checkable proofs of constant query complexity and logarithmic randomness complexity .The PCP theorem says that for some universal constant K, for every...
must be true.
Theorem 2
Håstad demonstrates a tighter result than Theorem 1 i.e. the best known value for ε.He constructs a PCP Verifier for 3-SAT that reads only 3 bits from the Proof.
For every ε > 0, there is a PCP-verifier M for 3-SAT that reads a random string r of length O(log(n)) and computes query positions ir, jr, kr in the proof π and a bit br. It accepts if and only if
π(ir) ⊕ π(jr) ⊕ π(kr) ⊕ = br.
The Verifier has completeness (1-ε) and soundness 1/2 + ε (refer to PCP (complexity)
PCP (complexity)
In computational complexity theory, a probabilistically checkable proof is a type of proof that can be checked by a randomized algorithm using a bounded amount of randomness and reading a bounded number of bits of the proof. The algorithm is then required to accept correct proofs and reject...
). The Verifier satisfies
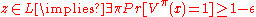
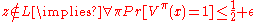
If the first of these two equations were equated to "=1" as usual, one could find a proof π by solving a system of linear equations (see MAX-3LIN-EQNMAX-3LIN-EQNMAX-3LIN-EQN is a problem in Computational complexity theory where the input is a system of linear equations . Each equation contains at most 3 variables. The problem is to find an assignment to the variables that satisfies the maximum number of equations.This problem is closely related to the...
) implying P = NP.
- If z ∈ L, a fraction ≥ (1- ε) of clauses are satisfied.
- If z ∉ L, then for a (1/2- ε) fraction of R, 1/4 clauses are contradicted.
This is enough to prove the hardness of approximation ratio
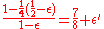
Related problems
MAX-3SAT(B) is the restricted special case of MAX-3SAT where every variable occurs in at most B clauses. Before the PCP theorem
PCP theorem
In computational complexity theory, the PCP theorem states that every decision problem in the NP complexity class has probabilistically checkable proofs of constant query complexity and logarithmic randomness complexity .The PCP theorem says that for some universal constant K, for every...
was proven, Papadimitriou and Yannakakis showed that for some fixed constant B, this problem is MAX SNP-hard. Consequently with the PCP theorem, it is also APX-hard. This is useful because MAX-3SAT(B) can often be used to obtain a PTAS-preserving reduction in a way that MAX-3SAT cannot. Proofs for explicit values of B include: all B ≥ 13, and all B ≥ 3 (which is best possible).
Moreover, although the decision problem 2SAT is solvable in polynomial time, MAX-2SAT(3) is also APX-hard.
The best possible approximation ratio for MAX-3SAT(B), as a function of B, is at least
 and at most
and at most 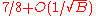 , unless NP=RP. Some explicit bounds on the approximability constants for certain values of B are known.
, unless NP=RP. Some explicit bounds on the approximability constants for certain values of B are known.MAX-EkSAT
MAXEkSAT
MAXEkSAT is a problem in computational complexity theory that is a maximization version of the Boolean satisfiability problem 3SAT.In MAXEkSAT, each clause has exactly k literals, with k ≥ 3, and is in conjunctive normal form...
is a paramaterized version of MAX-3SAT where every clause has exactly
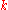 literals, for k ≥ 3. It can be efficiently approximated with approximation ratio
literals, for k ≥ 3. It can be efficiently approximated with approximation ratio 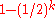 using ideas from coding theory.
using ideas from coding theory.

