
M-spline
Encyclopedia
In the mathematical
subfield of numerical analysis
, an M-spline is a non-negative spline
function.
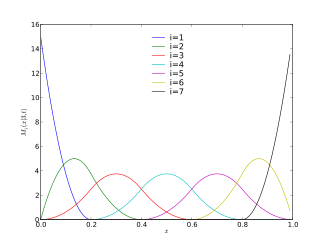
The family includes n members indexed by i = 1,...,n.
For k = 1,
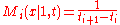
if ti ≤ x < ti+1, and Mi(x|1,t) = 0 otherwise.
For k > 1,

s. M-splines can also be used directly as basis splines for regression analysis involving positive response data (constraining the regression coefficients to be non-negative).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
subfield of numerical analysis
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
, an M-spline is a non-negative spline
Spline (mathematics)
In mathematics, a spline is a sufficiently smooth piecewise-polynomial function. In interpolating problems, spline interpolation is often preferred to polynomial interpolation because it yields similar results, even when using low-degree polynomials, while avoiding Runge's phenomenon for higher...
function.

Definition
A family of M-spline functions of order k with n free parameters is defined by a set of knots t1 ≤ t2 ≤ ... ≤ tn+k such that- t1 = ... = tk
- tn+1 = ... = tn+k
- ti < ti+k for all i
The family includes n members indexed by i = 1,...,n.
Properties
An M-spline Mi(x|k, t) has the following mathematical properties- Mi(x|k, t) is non-negative
- Mi(x|k, t) is zero unless ti ≤ x < ti+k
- Mi(x|k, t) has k − 2 continuous derivatives at interior knots tk+1, ..., tn−1
- Mi(x|k, t) integrates to 1
Computation
M-splines can be efficiently and stably computed using the following recursions:For k = 1,
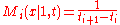
if ti ≤ x < ti+1, and Mi(x|1,t) = 0 otherwise.
For k > 1,

Applications
M-splines can be integrated to produce a family of monotone splines called I-splineI-spline
In the mathematical subfield of numerical analysis, an I-spline is a monotone spline function.-Definition:A family of I-spline functions of order k with n free parameters is defined in terms of the M-splines Mi...
s. M-splines can also be used directly as basis splines for regression analysis involving positive response data (constraining the regression coefficients to be non-negative).

