Lozanic's triangle
Encyclopedia
Lozanić's triangle is a triangular array
of binomial coefficient
s in a manner very similar to that of Pascal's triangle
. It is named after the Serbian chemist Sima Lozanić
, who researched it in his investigation into the symmetries exhibited by rows of paraffin
s.
The first few lines of Lozanić's triangle are
1
1 1
1 1 1
1 2 2 1
1 2 4 2 1
1 3 6 6 3 1
1 3 9 10 9 3 1
1 4 12 19 19 12 4 1
1 4 16 28 38 28 16 4 1
1 5 20 44 66 66 44 20 5 1
1 5 25 60 110 126 110 60 25 5 1
1 6 30 85 170 236 236 170 85 30 6 1
1 6 36 110 255 396 472 396 255 110 36 6 1
1 7 42 146 365 651 868 868 651 365 146 42 7 1
1 7 49 182 511 1001 1519 1716 1519 1001 511 182 49 7 1
1 8 56 231 693 1512 2520 3235 3235 2520 1512 693 231 56 8 1
listed in .
Like Pascal's triangle, outer edge diagonals of Lozanić's triangle are all 1s, and most of the enclosed numbers are the sum of the two numbers above. But for numbers at odd positions k in even-numbered rows n (starting the numbering for both with 0), after adding the two numbers above, subtract the number at position (k − 1)/2 in row n/2 − 1 of Pascal's triangle.
The diagonals next to the edge diagonals contain the positive integers in order, but with each integer stated twice .
Moving inwards, the next pair of diagonals contain the "quarter-squares" , or the square number
s and pronic number
s interleaved.
The next pair of diagonals contain the alkane numbers l(6, n) . And the next pair of diagonals contain the alkane numbers l(7, n) , while the next pair has the alkane numbers l(8, n) , then alkane numbers l(9, n) , then l(10, n) , l(11, n) , l(12, n) , etc.
The sum of the nth row of Lozanić's triangle is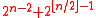
( lists the first thirty values or so).
The sums of the diagonals of Lozanić's triangle intermix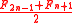
with 
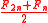(where Fx is the xth Fibonacci number
).
As expected, laying Pascal's triangle over Lozanić's triangle and subtracting yields a triangle with the outer diagonals consisting of zeroes . This particular difference triangle has applications in the chemical study of catacondensed polygonal systems.
Triangular array
In mathematics and computing, a triangular array of numbers, polynomials, or the like, is a doubly indexed sequence in which each row is only as long as the row's own index.Notable particular examples include these:...
of binomial coefficient
Binomial coefficient
In mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
s in a manner very similar to that of Pascal's triangle
Pascal's triangle
In mathematics, Pascal's triangle is a triangular array of the binomial coefficients in a triangle. It is named after the French mathematician, Blaise Pascal...
. It is named after the Serbian chemist Sima Lozanić
Sima Lozanic
Sima Lozanić was a Serbian chemist, president of the Serbian Royal Academy, the first rector of the University of Belgrade, minister of foreign affairs, minister of industry and diplomat.-Biography:...
, who researched it in his investigation into the symmetries exhibited by rows of paraffin
Paraffin
In chemistry, paraffin is a term that can be used synonymously with "alkane", indicating hydrocarbons with the general formula CnH2n+2. Paraffin wax refers to a mixture of alkanes that falls within the 20 ≤ n ≤ 40 range; they are found in the solid state at room temperature and begin to enter the...
s.
The first few lines of Lozanić's triangle are
1
1 1
1 1 1
1 2 2 1
1 2 4 2 1
1 3 6 6 3 1
1 3 9 10 9 3 1
1 4 12 19 19 12 4 1
1 4 16 28 38 28 16 4 1
1 5 20 44 66 66 44 20 5 1
1 5 25 60 110 126 110 60 25 5 1
1 6 30 85 170 236 236 170 85 30 6 1
1 6 36 110 255 396 472 396 255 110 36 6 1
1 7 42 146 365 651 868 868 651 365 146 42 7 1
1 7 49 182 511 1001 1519 1716 1519 1001 511 182 49 7 1
1 8 56 231 693 1512 2520 3235 3235 2520 1512 693 231 56 8 1
listed in .
Like Pascal's triangle, outer edge diagonals of Lozanić's triangle are all 1s, and most of the enclosed numbers are the sum of the two numbers above. But for numbers at odd positions k in even-numbered rows n (starting the numbering for both with 0), after adding the two numbers above, subtract the number at position (k − 1)/2 in row n/2 − 1 of Pascal's triangle.
The diagonals next to the edge diagonals contain the positive integers in order, but with each integer stated twice .
Moving inwards, the next pair of diagonals contain the "quarter-squares" , or the square number
Square number
In mathematics, a square number, sometimes also called a perfect square, is an integer that is the square of an integer; in other words, it is the product of some integer with itself...
s and pronic number
Pronic number
A pronic number, oblong number, rectangular number or heteromecic number, is a number which is the product of two consecutive integers, that is, n . The n-th pronic number is twice the n-th triangular number and n more than the n-th square number...
s interleaved.
The next pair of diagonals contain the alkane numbers l(6, n) . And the next pair of diagonals contain the alkane numbers l(7, n) , while the next pair has the alkane numbers l(8, n) , then alkane numbers l(9, n) , then l(10, n) , l(11, n) , l(12, n) , etc.
The sum of the nth row of Lozanić's triangle is
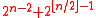( lists the first thirty values or so).The sums of the diagonals of Lozanić's triangle intermix
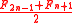with 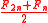(where Fx is the xth Fibonacci numberFibonacci number
In mathematics, the Fibonacci numbers are the numbers in the following integer sequence:0,\;1,\;1,\;2,\;3,\;5,\;8,\;13,\;21,\;34,\;55,\;89,\;144,\; \ldots\; ....
).
As expected, laying Pascal's triangle over Lozanić's triangle and subtracting yields a triangle with the outer diagonals consisting of zeroes . This particular difference triangle has applications in the chemical study of catacondensed polygonal systems.