Loss tangent
Encyclopedia
The loss tangent is a parameter of a dielectric material that quantifies its inherent dissipation of electromagnetic energy. The term refers to the tangent of the angle in a complex
plane between the resistive
(lossy) component of an electromagnetic field and its reactive (lossless) component.
, in a microstrip
line, or through a waveguide
. Dielectrics are often used in all of these environments to mechanically support electrical conductors and keep them at a fixed separation, or to provide a barrier between different gas pressures yet still transmit electromagnetic power. Maxwell’s equations are solved for the electric and magnetic field components of the propagating waves that satisfy the boundary conditions of the specific environment's geometry. In such electromagnetic analyses, the parameters permittivity
ε, permeability
μ, and conductivity σ represent the properties of the media through which the waves propagate. The permittivity can have real and imaginary components such that
.
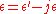If we assume that we have a wave function such that
,
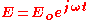then Maxwell's curl equation for the magnetic field can be written as
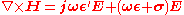
where ε″ is the imaginary amplitude of permittivity attributed to bound charge and dipole relaxation phenomena, which gives rise to energy loss that is indistinguishable from the loss due to the free charge conduction that is quantified by σ. The component ε′ represents the familiar lossless permittivity given by the product of the free space permittivity and the relative permittivity, or ε′ = ε0 εr. The loss tangent is then defined as the ratio (or angle in a complex plane) of the lossy reaction to the electric field E in the curl equation to the lossless reaction:
.
For dielectrics with small loss, this angle is ≪ 1 and tan δ ≈ δ. After some further maths to obtain the solution for the fields of the electromagnetic wave, it turns out that the power decays with propagation distance z as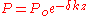
, where
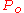is the initial power,
,
There are often other contributions to power loss for electromagnetic waves that are not included in this expression, such as due to the wall currents of the conductors of a transmission line or waveguide. Also, a similar analysis could be applied to the permeability where
,
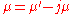with the subsequent definition of a magnetic loss tangent
.
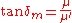is typically made of a dielectric placed between conductors. The lumped element model
of a capacitor includes a lossless ideal capacitor in series with a resistor termed the equivalent series resistance
(ESR), as shown in the figure below. The ESR represents losses in the capacitor. In a low-loss capacitor the ESR is very small, and in a lossy capacitor the ESR can be large. Note that the ESR is not simply the resistance that would be measured across a capacitor by an ohmmeter
. The ESR is a derived quantity representing the loss due to both the dielectric's conduction electrons and the bound dipole relaxation phenomena mentioned above. In a dielectric, only one of either the conduction electrons or the dipole relaxation typically dominates loss. For the case of the conduction electrons being the dominant loss, then
,
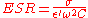where
is the lossless capacitance.
When representing the electrical circuit parameters as vectors in a complex
plane, known as phasors, a capacitor's loss tangent is equal to the tangent of the angle between the capacitor's impedance vector and the negative reactive axis, as shown in the diagram to the right. The loss tangent is then
.
Since the same AC
current flows through both ESR and Xc, the loss tangent is also the ratio of the resistive
power loss in the ESR to the reactive power oscillating in the capacitor. For this reason, a capacitor's loss tangent is sometimes stated as its dissipation factor
, or the reciprocal of its quality factor Q, as follows
.
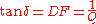Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
plane between the resistive
Electrical resistance
The electrical resistance of an electrical element is the opposition to the passage of an electric current through that element; the inverse quantity is electrical conductance, the ease at which an electric current passes. Electrical resistance shares some conceptual parallels with the mechanical...
(lossy) component of an electromagnetic field and its reactive (lossless) component.
Electromagnetic field perspective
For time varying electromagnetic fields, the electromagnetic energy is typically viewed as waves propagating either through free space, in a transmission lineTransmission line
In communications and electronic engineering, a transmission line is a specialized cable designed to carry alternating current of radio frequency, that is, currents with a frequency high enough that its wave nature must be taken into account...
, in a microstrip
Microstrip
Microstrip is a type of electrical transmission line which can be fabricated using printed circuit board technology, and is used to convey microwave-frequency signals. It consists of a conducting strip separated from a ground plane by a dielectric layer known as the substrate. Microwave components...
line, or through a waveguide
Waveguide
A waveguide is a structure which guides waves, such as electromagnetic waves or sound waves. There are different types of waveguides for each type of wave...
. Dielectrics are often used in all of these environments to mechanically support electrical conductors and keep them at a fixed separation, or to provide a barrier between different gas pressures yet still transmit electromagnetic power. Maxwell’s equations are solved for the electric and magnetic field components of the propagating waves that satisfy the boundary conditions of the specific environment's geometry. In such electromagnetic analyses, the parameters permittivity
Permittivity
In electromagnetism, absolute permittivity is the measure of the resistance that is encountered when forming an electric field in a medium. In other words, permittivity is a measure of how an electric field affects, and is affected by, a dielectric medium. The permittivity of a medium describes how...
ε, permeability
Permeability (electromagnetism)
In electromagnetism, permeability is the measure of the ability of a material to support the formation of a magnetic field within itself. In other words, it is the degree of magnetization that a material obtains in response to an applied magnetic field. Magnetic permeability is typically...
μ, and conductivity σ represent the properties of the media through which the waves propagate. The permittivity can have real and imaginary components such that
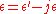.If we assume that we have a wave function such that
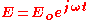,then Maxwell's curl equation for the magnetic field can be written as
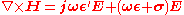
where ε″ is the imaginary amplitude of permittivity attributed to bound charge and dipole relaxation phenomena, which gives rise to energy loss that is indistinguishable from the loss due to the free charge conduction that is quantified by σ. The component ε′ represents the familiar lossless permittivity given by the product of the free space permittivity and the relative permittivity, or ε′ = ε0 εr. The loss tangent is then defined as the ratio (or angle in a complex plane) of the lossy reaction to the electric field E in the curl equation to the lossless reaction:
.For dielectrics with small loss, this angle is ≪ 1 and tan δ ≈ δ. After some further maths to obtain the solution for the fields of the electromagnetic wave, it turns out that the power decays with propagation distance z as
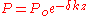, where 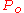is the initial power,,
- ω is the angular frequency of the wave, and
- λ is the wavelength in the dielectric.
There are often other contributions to power loss for electromagnetic waves that are not included in this expression, such as due to the wall currents of the conductors of a transmission line or waveguide. Also, a similar analysis could be applied to the permeability where
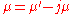,with the subsequent definition of a magnetic loss tangent
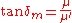.Discrete circuit perspective
For discrete electrical circuit components, a capacitorCapacitor
A capacitor is a passive two-terminal electrical component used to store energy in an electric field. The forms of practical capacitors vary widely, but all contain at least two electrical conductors separated by a dielectric ; for example, one common construction consists of metal foils separated...
is typically made of a dielectric placed between conductors. The lumped element model
Lumped element model
The lumped element model simplifies the description of the behaviour of spatially distributed physical systems into a topology consisting of discrete entities that approximate the behaviour of the distributed system under certain assumptions...
of a capacitor includes a lossless ideal capacitor in series with a resistor termed the equivalent series resistance
Equivalent series resistance
Practical capacitors and inductors as used in electric circuits are not ideal components with only capacitance or inductance. However, they can be treated to a very good approximation as ideal capacitors and inductors in series with a resistance; this resistance is defined to be the equivalent...
(ESR), as shown in the figure below. The ESR represents losses in the capacitor. In a low-loss capacitor the ESR is very small, and in a lossy capacitor the ESR can be large. Note that the ESR is not simply the resistance that would be measured across a capacitor by an ohmmeter
Ohmmeter
An ohmmeter is an electrical instrument that measures electrical resistance, the opposition to an electric current. Micro-ohmmeters make low resistance measurements. Megohmmeters measure large values of resistance...
. The ESR is a derived quantity representing the loss due to both the dielectric's conduction electrons and the bound dipole relaxation phenomena mentioned above. In a dielectric, only one of either the conduction electrons or the dipole relaxation typically dominates loss. For the case of the conduction electrons being the dominant loss, then
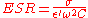,where
is the lossless capacitance.When representing the electrical circuit parameters as vectors in a complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
plane, known as phasors, a capacitor's loss tangent is equal to the tangent of the angle between the capacitor's impedance vector and the negative reactive axis, as shown in the diagram to the right. The loss tangent is then
.Since the same AC
Alternating current
In alternating current the movement of electric charge periodically reverses direction. In direct current , the flow of electric charge is only in one direction....
current flows through both ESR and Xc, the loss tangent is also the ratio of the resistive
Electrical resistance
The electrical resistance of an electrical element is the opposition to the passage of an electric current through that element; the inverse quantity is electrical conductance, the ease at which an electric current passes. Electrical resistance shares some conceptual parallels with the mechanical...
power loss in the ESR to the reactive power oscillating in the capacitor. For this reason, a capacitor's loss tangent is sometimes stated as its dissipation factor
Dissipation factor
In physics, the dissipation factor is a measure of loss-rate of energy of a mode of oscillation in a dissipative system. It is the reciprocal of Quality factor, which represents the quality of oscillation....
, or the reciprocal of its quality factor Q, as follows
.
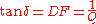