
Log sum inequality
Encyclopedia
In mathematics, the log sum inequality is an inequality which is useful for proving several theorems in information theory
.
 and
and  be nonnegative numbers. Denote the sum of all
be nonnegative numbers. Denote the sum of all  s by
s by  and the sum of all
and the sum of all 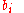 s by
s by  . The log sum inequality states that
. The log sum inequality states that
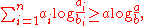
with equality if and only if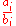 are equal for all
are equal for all 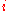 .
.
 we have
we have
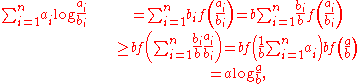
where the inequality follows from Jensen's inequality
since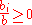 ,
, 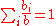 , and
, and  is convex.
is convex.
or the convexity of Kullback-Leibler divergence.
For example to prove Gibbs' inequality it is enough to substitute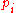 s for
s for  s, and
s, and  s for
s for 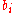 s to get
s to get
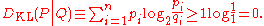
 provided that
provided that  and
and  .
.
Generalizations to convex functions other than the logarithm is given in Csiszár, 2004.
Information theory
Information theory is a branch of applied mathematics and electrical engineering involving the quantification of information. Information theory was developed by Claude E. Shannon to find fundamental limits on signal processing operations such as compressing data and on reliably storing and...
.
Statement
Let and
and  be nonnegative numbers. Denote the sum of all
be nonnegative numbers. Denote the sum of all  s by
s by  and the sum of all
and the sum of all 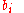 s by
s by  . The log sum inequality states that
. The log sum inequality states that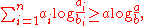
with equality if and only if
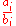 are equal for all
are equal for all 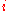 .
.Proof
Notice that after setting we have
we have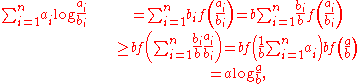
where the inequality follows from Jensen's inequality
Jensen's inequality
In mathematics, Jensen's inequality, named after the Danish mathematician Johan Jensen, relates the value of a convex function of an integral to the integral of the convex function. It was proved by Jensen in 1906. Given its generality, the inequality appears in many forms depending on the context,...
since
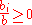 ,
, 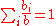 , and
, and  is convex.
is convex.Applications
The log sum inequality can be used to prove several inequalities in information theory such as Gibbs' inequalityGibbs' inequality
In information theory, Gibbs' inequality is a statement about the mathematical entropy of a discrete probability distribution. Several other bounds on the entropy of probability distributions are derived from Gibbs' inequality, including Fano's inequality....
or the convexity of Kullback-Leibler divergence.
For example to prove Gibbs' inequality it is enough to substitute
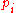 s for
s for  s, and
s, and  s for
s for 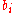 s to get
s to get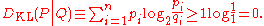
Generalizations
The inequality remains valid for provided that
provided that  and
and  .
.Generalizations to convex functions other than the logarithm is given in Csiszár, 2004.

