List update problem
Encyclopedia
The List Update or the List Access problem is a simple model used in the study of competitive analysis
of online algorithms. Given a set of items in a list where the cost of accessing an item is proportional to its distance from the head of the list, e.g a Linked List
, and a request sequence of accesses, the problem is to come up with a strategy of reordering the list so that the total cost of accesses is minimized. The reordering can be done at any time but incurs a cost, and the standard cost model includes a free transposition of the item being accessed anywhere ahead of its current position and a paid transposition of a unit cost for exchanging any two items in the list. Performance of algorithms depend on the construction of request sequences by adversaries under various Adversary models
An online algorithm for this problem has to reorder the elements and serve requests based only on the knowledge of previously requested items and hence its strategy may not have the optimum cost as compared to an offline algorithm that gets to see the entire request sequence and device a complete strategy before serving the first request.
for an algorithm ALG. Depending of whether 
can be changed based on the strategy of ALG, adversaries are given various powers, and the performance of ALG is measured against these adversaries.
An oblivious adversary has to construct the entire request sequence
before running ALG, and pays the optimal offline price,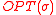 
which is compared against 
An adaptive online adversary gets to make the next request based on the previous results of the online algorithm, but pays for the request optimally and online.
An adaptive offline adversary gets to make the next request based on the previous results of the online algorithm, but pays the optimal offline cost.
It is interesting to note that paid transpositions are in general necessary for optimum algorithms. Consider a list (a,b,c) where a is at the head of the list, and a request sequence c,b,c,b. An optimal offline algorithm using only free exchanges would cost 9 (3+3+2+1), where as an optimal offline algorithm using only paid exchanges would cost 7 (Swap c and a in the beginning = 1+(1+2+1+2)). So, we cannot get away with just using free transpositions for the optimum offline algorithm.
The optimum list update problem was proven to be NP-Hard
by .
such that for all finite length request sequences 
, 
. Online algorithms can either be deterministic or randomized and it turns out that randomization in this case can truly help against oblivious adversaries.
MTF (Move to front) : After accessing an item move it to the front of the list without changing the order of other items
TRANS (Transpose) : After accessing an item, transpose it with the immediately preceding item.
FC (Frequency Count) : For each item maintain a frequency count of the number of accesses to it - when an element is accessed increase its frequency count and reorder the list in the decreasing order of frequencies.
Observe that all these use just free transpositions. It turns out that both TRANS and FC are not competitive. In a classic result using Potential method
analysis proved that MTF is 2-competitive. The proof does not require the explicit knowledge of OPT but instead counts the number of inversions i.e elements occurring in opposite order in the lists of MTF and OPT.
Any deterministic algorithm has a lower bound of
for a list of length l, and MTF is actually the optimum deterministic list update algorithm. The type of adversary doesn't matter in the case of deterministic algorithms, because the adversary can run a copy of the deterministic algorithm on his own to precompute the most disastrous sequence.
BIT : For every item in the list, maintain a bit. Initialize all the bits uniformly and randomly to 0 or 1. When an item is accessed, flip the bit, and if it is 1 move it to the front, else don't.
This algorithm is barely random - it makes all its random choices in the beginning and not during the run. It turns out that BIT breaks the deterministic bound - it is better than MTF against oblivious adversaries. It is 7/4-competitive. There are other randomized algorithms, like COMB, that perform better than BIT. Teia proved a lower bound of 1.5 for any randomized list update algorithm.
holds for the dynamic model as well.
There are different cost models as well. In the usual full cost model, an access to an element located at a position i costs i, but the last comparison is inevitable for any algorithm, i.e there are i-1 elements standing in the way of i. In the partial cost model, these final comparison costs totaling to the number of elements in the request sequence are ignored. For the costs of paid transpositions other than unity, Pd models are used.
Competitive analysis (online algorithm)
Competitive analysis is a method invented for analyzing online algorithms, in which the performance of an online algorithm is compared to the performance of an optimal offline algorithm that can view the sequence of requests in advance...
of online algorithms. Given a set of items in a list where the cost of accessing an item is proportional to its distance from the head of the list, e.g a Linked List
Linked list
In computer science, a linked list is a data structure consisting of a group of nodes which together represent a sequence. Under the simplest form, each node is composed of a datum and a reference to the next node in the sequence; more complex variants add additional links...
, and a request sequence of accesses, the problem is to come up with a strategy of reordering the list so that the total cost of accesses is minimized. The reordering can be done at any time but incurs a cost, and the standard cost model includes a free transposition of the item being accessed anywhere ahead of its current position and a paid transposition of a unit cost for exchanging any two items in the list. Performance of algorithms depend on the construction of request sequences by adversaries under various Adversary models
An online algorithm for this problem has to reorder the elements and serve requests based only on the knowledge of previously requested items and hence its strategy may not have the optimum cost as compared to an offline algorithm that gets to see the entire request sequence and device a complete strategy before serving the first request.
Adversary Models
An adversary is an entity that gets to choose the request sequence for an algorithm ALG. Depending of whether can be changed based on the strategy of ALG, adversaries are given various powers, and the performance of ALG is measured against these adversaries.An oblivious adversary has to construct the entire request sequence
before running ALG, and pays the optimal offline price, 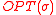which is compared against An adaptive online adversary gets to make the next request based on the previous results of the online algorithm, but pays for the request optimally and online.
An adaptive offline adversary gets to make the next request based on the previous results of the online algorithm, but pays the optimal offline cost.
Offline algorithms
Competitive analysis for many list update problems were carried out without any specific knowledge of the exact nature of the optimum offline algorithm (OPT). The best known algorithm runs in O(n2l(l-1)!) time and O(l!) space where n is the length of the request sequence and l is the length of the list.It is interesting to note that paid transpositions are in general necessary for optimum algorithms. Consider a list (a,b,c) where a is at the head of the list, and a request sequence c,b,c,b. An optimal offline algorithm using only free exchanges would cost 9 (3+3+2+1), where as an optimal offline algorithm using only paid exchanges would cost 7 (Swap c and a in the beginning = 1+(1+2+1+2)). So, we cannot get away with just using free transpositions for the optimum offline algorithm.
The optimum list update problem was proven to be NP-Hard
NP-hard
NP-hard , in computational complexity theory, is a class of problems that are, informally, "at least as hard as the hardest problems in NP". A problem H is NP-hard if and only if there is an NP-complete problem L that is polynomial time Turing-reducible to H...
by .
Online algorithm
An online algorithm ALG has a competitive ratio c if for any input it performs at least as good as c times worse than OPT. i.e if there exists an such that for all finite length request sequences , . Online algorithms can either be deterministic or randomized and it turns out that randomization in this case can truly help against oblivious adversaries.Deterministic
Most deterministic algorithms are variants of these three algorithms :MTF (Move to front) : After accessing an item move it to the front of the list without changing the order of other items
TRANS (Transpose) : After accessing an item, transpose it with the immediately preceding item.
FC (Frequency Count) : For each item maintain a frequency count of the number of accesses to it - when an element is accessed increase its frequency count and reorder the list in the decreasing order of frequencies.
Observe that all these use just free transpositions. It turns out that both TRANS and FC are not competitive. In a classic result using Potential method
Potential method
In computational complexity theory, the potential method is a method used to analyze the amortized time and space complexity of a data structure, a measure of its performance over sequences of operations that smooths out the cost of infrequent but expensive operations.-Definition of amortized...
analysis proved that MTF is 2-competitive. The proof does not require the explicit knowledge of OPT but instead counts the number of inversions i.e elements occurring in opposite order in the lists of MTF and OPT.
Any deterministic algorithm has a lower bound of
for a list of length l, and MTF is actually the optimum deterministic list update algorithm. The type of adversary doesn't matter in the case of deterministic algorithms, because the adversary can run a copy of the deterministic algorithm on his own to precompute the most disastrous sequence.Randomized
Consider the following simple randomized algorithm :BIT : For every item in the list, maintain a bit. Initialize all the bits uniformly and randomly to 0 or 1. When an item is accessed, flip the bit, and if it is 1 move it to the front, else don't.
This algorithm is barely random - it makes all its random choices in the beginning and not during the run. It turns out that BIT breaks the deterministic bound - it is better than MTF against oblivious adversaries. It is 7/4-competitive. There are other randomized algorithms, like COMB, that perform better than BIT. Teia proved a lower bound of 1.5 for any randomized list update algorithm.
Related Problems
The list update problem where elements maybe inserted and deleted is called the dynamic list update problem, as opposed to the static list update problem where only accessing list elements are allowed. The upper bound of holds for the dynamic model as well.There are different cost models as well. In the usual full cost model, an access to an element located at a position i costs i, but the last comparison is inevitable for any algorithm, i.e there are i-1 elements standing in the way of i. In the partial cost model, these final comparison costs totaling to the number of elements in the request sequence are ignored. For the costs of paid transpositions other than unity, Pd models are used.
See also
- Online algorithmOnline algorithmIn computer science, an online algorithm is one that can process its input piece-by-piece in a serial fashion, i.e., in the order that the input is fed to the algorithm, without having the entire input available from the start. In contrast, an offline algorithm is given the whole problem data from...
- Competitive analysisCompetitive analysis (online algorithm)Competitive analysis is a method invented for analyzing online algorithms, in which the performance of an online algorithm is compared to the performance of an optimal offline algorithm that can view the sequence of requests in advance...
- Cache algorithmsCache algorithmsIn computing, cache algorithms are optimizing instructions – algorithms – that a computer program or a hardware-maintained structure can follow to manage a cache of information stored on the computer...