
Lindeberg's condition
Encyclopedia
In probability theory
, Lindeberg's condition is a sufficient condition (and under certain conditions also a necessary condition) for the central limit theorem
to hold for a sequence of independent random variables. Unlike the classical central limit theorem, which requires that the random variables in question to have finite mean
and variance
and be both independent and identically distributed, it only requires that they have finite mean and variance and be independent
. It is named after the Finnish mathematician Jarl Waldemar Lindeberg
.
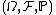 be a probability space
be a probability space
, and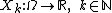 , be independent random variables defined on that space. Assume the expected values
, be independent random variables defined on that space. Assume the expected values 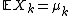 and variances
and variances 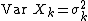 exist and are finite. Also let
exist and are finite. Also let 
If this sequence of independent random variables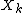 satisfies the Lindeberg's condition:
satisfies the Lindeberg's condition:
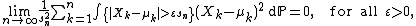
(where the integral is a Lebesgue integral over the set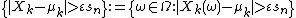 ), then the central limit theorem
), then the central limit theorem
holds, i.e. the random variable

converges in distribution to a standard normal random variable as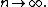
Lindeberg's condition is sufficient, but not in general necessary (i.e. the inverse implication does not hold in general).
However, if the sequence of independent random variables in question satisfies
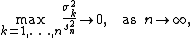
then Lindeberg's condition is both sufficient and necessary, i.e. it holds if and only if the result of central limit theorem
holds.
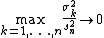 as
as  , it guarantees that the contribution of any individual random variable
, it guarantees that the contribution of any individual random variable 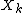 (
( ) to the variance
) to the variance  is arbitrarily small, for sufficiently large values of
is arbitrarily small, for sufficiently large values of  .
.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, Lindeberg's condition is a sufficient condition (and under certain conditions also a necessary condition) for the central limit theorem
Central limit theorem
In probability theory, the central limit theorem states conditions under which the mean of a sufficiently large number of independent random variables, each with finite mean and variance, will be approximately normally distributed. The central limit theorem has a number of variants. In its common...
to hold for a sequence of independent random variables. Unlike the classical central limit theorem, which requires that the random variables in question to have finite mean
Mean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
and variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
and be both independent and identically distributed, it only requires that they have finite mean and variance and be independent
Statistical independence
In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
. It is named after the Finnish mathematician Jarl Waldemar Lindeberg
Jarl Waldemar Lindeberg
Jarl Waldemar Lindeberg was a Finnish mathematician known for work on the central limit theorem....
.
Statement
Let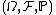 be a probability space
be a probability spaceProbability space
In probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...
, and
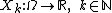 , be independent random variables defined on that space. Assume the expected values
, be independent random variables defined on that space. Assume the expected values 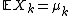 and variances
and variances 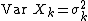 exist and are finite. Also let
exist and are finite. Also let 
If this sequence of independent random variables
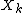 satisfies the Lindeberg's condition:
satisfies the Lindeberg's condition: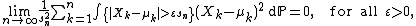
(where the integral is a Lebesgue integral over the set
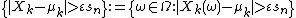 ), then the central limit theorem
), then the central limit theoremCentral limit theorem
In probability theory, the central limit theorem states conditions under which the mean of a sufficiently large number of independent random variables, each with finite mean and variance, will be approximately normally distributed. The central limit theorem has a number of variants. In its common...
holds, i.e. the random variable

converges in distribution to a standard normal random variable as
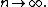
Lindeberg's condition is sufficient, but not in general necessary (i.e. the inverse implication does not hold in general).
However, if the sequence of independent random variables in question satisfies
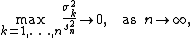
then Lindeberg's condition is both sufficient and necessary, i.e. it holds if and only if the result of central limit theorem
Central limit theorem
In probability theory, the central limit theorem states conditions under which the mean of a sufficiently large number of independent random variables, each with finite mean and variance, will be approximately normally distributed. The central limit theorem has a number of variants. In its common...
holds.
Interpretation
Because, the Lindeberg condition implies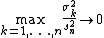 as
as  , it guarantees that the contribution of any individual random variable
, it guarantees that the contribution of any individual random variable 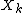 (
( ) to the variance
) to the variance  is arbitrarily small, for sufficiently large values of
is arbitrarily small, for sufficiently large values of  .
.

