Limiting parallel
Encyclopedia
In neutral geometry
, there may be many lines parallel to a given line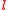
at a point 
, however one parallel may be closer to 
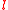than all others. Thus it is useful to make a new definition concerning parallels in neutral geometry. If there is a closest parallel to a given line it is known at the limiting parallel.
The relation of limiting parallel for rays is an equivalence relation
, which includes the equivalence relation of being coterminal.
Limiting parallels may sometimes form two, or three sides of a limit triangle.
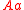is a limiting parallel to a ray 
if they are coterminal or if they lie on distinct lines not equal to the line 
, they do not meet, and every ray in the interior of the angle 
meets the ray 
.
which either 
is on. Then they must meet on the side of 
opposite to 
, call this point 
. Thus 
. Contradiction.
Absolute geometry
Absolute geometry is a geometry based on an axiom system for Euclidean geometry that does not assume the parallel postulate or any of its alternatives. The term was introduced by János Bolyai in 1832...
, there may be many lines parallel to a given line
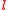at a point , however one parallel may be closer to 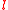than all others. Thus it is useful to make a new definition concerning parallels in neutral geometry. If there is a closest parallel to a given line it is known at the limiting parallel.The relation of limiting parallel for rays is an equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
, which includes the equivalence relation of being coterminal.
Limiting parallels may sometimes form two, or three sides of a limit triangle.
Definition
A ray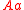 is a limiting parallel to a ray if they are coterminal or if they lie on distinct lines not equal to the line , they do not meet, and every ray in the interior of the angle meets the ray .Proof
Suppose that the lines carrying distinct parallel rays met. By definition the cannot meet on the side of which either is on. Then they must meet on the side of opposite to , call this point . Thus . Contradiction.