Liberal paradox
Encyclopedia
The liberal paradox is a logical paradox
advanced by Amartya Sen
, building on the work of Kenneth Arrow
and his impossibility theorem
, which showed that within a system of menu-independent social choice, it is impossible to have both a commitment to "Minimal Liberty", which was defined as the ability to order tuple
s of choices, and Pareto optimality.
Since this theorem was advanced in 1970, it has attracted a wide body of commentary from philosophers such as James M. Buchanan
and Robert Nozick
.
The most contentious aspect is, on one hand, to contradict the libertarian
notion that the market mechanism is sufficient to produce a Pareto-optimal society—and on the other hand, argue that degrees of choice and freedom, rather than welfare economics
, should be the defining trait of that market mechanism. As a result it attracts commentary from both the left and the right of the political spectrum.
Suppose there is a set of social outcomes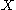
with at least two alternatives and there is a group of at least two individuals each with preferences 
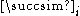over 
.
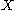A benign social planner has to choose a single outcome from the set using the information about the individuals' preferences. The planner uses a social choice function. For every possible set of preferences, a social choice function selects a choice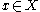
.
There are two desirable properties we might ask of the social choice function:
That is, there is one individual called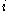
and one pair of alternatives 
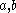such that if 
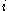strictly prefers 
to 
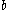then the social choice function cannot chose 
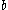and vice-versa.
Similarly there must be another individual called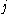
whose preferences can veto a choice over a (possibly different) pair of alternatives 
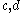. If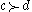 
then the social choice function cannot select 
.
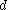Sen's impossibility theorem establishes that it's impossible for the social planner to satisfy condition 1 and condition 2. In other words, for every social choice function there is at least one set of preferences that force the planner to violate condition (1) or condition (2).
Suppose that we give each individual the right to decide whether they want or don't want to read the book. Then it's impossible to find a social choice function without violating "Minimal liberalism" or the "Paretian principle". "Minimal liberalism" requires that Mr. 1 not be forced to read the book, so
cannot be chosen. It also requires that Mr. 2 not be forbidden from reading the book, so 
cannot be chosen. But alternative 
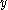cannot be chosen either because of the Paretian principle. Both Mr. 1 and Mr. 2 agree that that they prefer Mr. 1 to read the book (
) than Mr. 2 (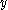
).
Since we have ruled out any possible solutions, we must conclude that it's impossible to find a social choice function.
have to decide whether to go to the cinema to see a 'chick flick
', and that each has the liberty to decide whether to go themselves. If the personal preferences are based on Alice first wanting to be with Bob, then thinking it is a good film, and on Bob first wanting Alice to see it but then not wanting to go himself, then the personal preference orders might be:
There are two Pareto efficient solutions: either Alice goes alone or they both go. Clearly Bob will not go on his own: he would not set off alone, but if he did then Alice would follow, and Alice's personal liberty means the joint preference must have both to go > Bob to go. However, since Alice also has personal liberty if Bob does not go, the joint preference must have neither to go > Alice to go. But Bob has personal liberty too, so the joint preference must have Alice to go > both to go and neither to go > Bob to go. Combining these gives
and in particular neither to go > both to go. So the result of these individual preferences and personal liberty is that neither go to see the film.
But this is Pareto inefficient given that Alice and Bob each think both to go > neither to go.
The diagram shows the strategy graphically. The numbers represent ranks in Alice and Bob's personal preferences, relevant for Pareto efficiency
(thus, either 4,3 or 2,4 is better than 1,1 and 4,3 is better than 3,2 – making 4,3 and 2,4 the two solutions). The arrows represent transitions suggested by the individual preferences over which each has liberty, clearly leading to the solution for neither to go.
Nevertheless, the general case will be that there are some externalities
. For instance, one individual is free to go to work by car or by bicycle. If the individual takes the car and drives to work, whereas society wants him to go to work by bicycle there will be an externality. However, no one can force the other to prefer cycling. So, one implication of Sen's paradox is that these externalities will exist wherever liberalism exists.
Taken all together all three ways do not resolve the paradox as such. But, they answer the question: What can society do, if the paradox applies and no corresponding social decision function can handle the trade off between Pareto-optimality and liberalism? One sees that mutual acceptance and self-constraints or even contracts to trade away actions or rights are needed.
Paradox
Similar to Circular reasoning, A paradox is a seemingly true statement or group of statements that lead to a contradiction or a situation which seems to defy logic or intuition...
advanced by Amartya Sen
Amartya Sen
Amartya Sen, CH is an Indian economist who was awarded the 1998 Nobel Prize in Economic Sciences for his contributions to welfare economics and social choice theory, and for his interest in the problems of society's poorest members...
, building on the work of Kenneth Arrow
Kenneth Arrow
Kenneth Joseph Arrow is an American economist and joint winner of the Nobel Memorial Prize in Economics with John Hicks in 1972. To date, he is the youngest person to have received this award, at 51....
and his impossibility theorem
Arrow's impossibility theorem
In social choice theory, Arrow’s impossibility theorem, the General Possibility Theorem, or Arrow’s paradox, states that, when voters have three or more distinct alternatives , no voting system can convert the ranked preferences of individuals into a community-wide ranking while also meeting a...
, which showed that within a system of menu-independent social choice, it is impossible to have both a commitment to "Minimal Liberty", which was defined as the ability to order tuple
Tuple
In mathematics and computer science, a tuple is an ordered list of elements. In set theory, an n-tuple is a sequence of n elements, where n is a positive integer. There is also one 0-tuple, an empty sequence. An n-tuple is defined inductively using the construction of an ordered pair...
s of choices, and Pareto optimality.
Since this theorem was advanced in 1970, it has attracted a wide body of commentary from philosophers such as James M. Buchanan
James M. Buchanan
James McGill Buchanan, Jr. is an American economist known for his work on public choice theory, for which he received the 1986 Nobel Memorial Prize in Economic Sciences. Buchanan's work initiated research on how politicians' self-interest and non-economic forces affect government economic policy...
and Robert Nozick
Robert Nozick
Robert Nozick was an American political philosopher, most prominent in the 1970s and 1980s. He was a professor at Harvard University. He is best known for his book Anarchy, State, and Utopia , a right-libertarian answer to John Rawls's A Theory of Justice...
.
The most contentious aspect is, on one hand, to contradict the libertarian
Libertarianism
Libertarianism, in the strictest sense, is the political philosophy that holds individual liberty as the basic moral principle of society. In the broadest sense, it is any political philosophy which approximates this view...
notion that the market mechanism is sufficient to produce a Pareto-optimal society—and on the other hand, argue that degrees of choice and freedom, rather than welfare economics
Welfare economics
Welfare economics is a branch of economics that uses microeconomic techniques to evaluate economic well-being, especially relative to competitive general equilibrium within an economy as to economic efficiency and the resulting income distribution associated with it...
, should be the defining trait of that market mechanism. As a result it attracts commentary from both the left and the right of the political spectrum.
The theorem
The formal statement of the theorem is as follows.Suppose there is a set of social outcomes
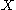with at least two alternatives and there is a group of at least two individuals each with preferences 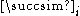over 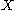.A benign social planner has to choose a single outcome from the set using the information about the individuals' preferences. The planner uses a social choice function. For every possible set of preferences, a social choice function selects a choice
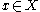.There are two desirable properties we might ask of the social choice function:
- A social choice function respects the Paretian principle (also called Pareto optimality) if it never selects an outcome when there is an alternative that everybody strictly prefers. So if there are two choices,
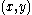such that 
for all individuals, then the social choice function does not select 
. - A social choice function respects minimal liberalism if there are two individuals whose preferences can veto some social outcomes.
That is, there is one individual called
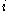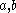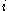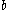and one pair of alternatives such that if strictly prefers to then the social choice function cannot chose 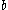and vice-versa.Similarly there must be another individual called
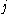whose preferences can veto a choice over a (possibly different) pair of alternatives 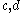. If 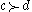then the social choice function cannot select 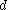.Sen's impossibility theorem establishes that it's impossible for the social planner to satisfy condition 1 and condition 2. In other words, for every social choice function there is at least one set of preferences that force the planner to violate condition (1) or condition (2).
Sen's example
The following simple example involving two agents and three alternatives was put forward by Sen.
There is a copy of a certain book, say Lady Chatterly's LoverLady Chatterley's LoverLady Chatterley's Lover is a novel by D. H. Lawrence, first published in 1928. The first edition was printed privately in Florence, Italy with assistance from Pino Orioli; it could not be published openly in the United Kingdom until 1960...
, which is viewed differently by individuals 1 and 2. The three alternatives are: that individual 1 reads it (), that individual 2 reads it (
), that no one reads it (
). Person 1, who is a prude, prefers most that no one reads it, but given the choice between either of the two reading it, he would prefer that he read it himself rather than exposing the gullible Mr. 2 to the influences of Lawrence. (Prudes, I am told, tend to prefer to be censors than being censored.) In decreasing order of preference, his ranking is
. Person 2, however, prefers that either of them should read it rather than neither. Furthermore he takes delight in the thought that prudish Mr. 1 may have to read Lawrence, and his first preference is that person 1 should read it, next best that he himself should read it, and worst that neither should. His ranking is, therefore,
.
Suppose that we give each individual the right to decide whether they want or don't want to read the book. Then it's impossible to find a social choice function without violating "Minimal liberalism" or the "Paretian principle". "Minimal liberalism" requires that Mr. 1 not be forced to read the book, so
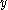cannot be chosen. It also requires that Mr. 2 not be forbidden from reading the book, so cannot be chosen. But alternative cannot be chosen either because of the Paretian principle. Both Mr. 1 and Mr. 2 agree that that they prefer Mr. 1 to read the book () than Mr. 2 (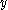).Since we have ruled out any possible solutions, we must conclude that it's impossible to find a social choice function.
Another example
Suppose Alice and BobAlice and Bob
The names Alice and Bob are commonly used placeholder names for archetypal characters in fields such as cryptography and physics. The names are used for convenience; for example, "Alice sends a message to Bob encrypted with his public key" is easier to follow than "Party A sends a message to Party...
have to decide whether to go to the cinema to see a 'chick flick
Chick flick
Chick flick is a slang term for a film mainly dealing with love and romance designed to appeal to a female target audience. Although many types of films may be directed toward the female gender, "chick flick" is typically used only in reference to films that are heavy with emotion or contain themes...
', and that each has the liberty to decide whether to go themselves. If the personal preferences are based on Alice first wanting to be with Bob, then thinking it is a good film, and on Bob first wanting Alice to see it but then not wanting to go himself, then the personal preference orders might be:
- Alice wants: both to go > neither to go > Alice to go > Bob to go
- Bob wants: Alice to go > both to go > neither to go > Bob to go
There are two Pareto efficient solutions: either Alice goes alone or they both go. Clearly Bob will not go on his own: he would not set off alone, but if he did then Alice would follow, and Alice's personal liberty means the joint preference must have both to go > Bob to go. However, since Alice also has personal liberty if Bob does not go, the joint preference must have neither to go > Alice to go. But Bob has personal liberty too, so the joint preference must have Alice to go > both to go and neither to go > Bob to go. Combining these gives
- Joint preference: neither to go > Alice to go > both to go > Bob to go
and in particular neither to go > both to go. So the result of these individual preferences and personal liberty is that neither go to see the film.
But this is Pareto inefficient given that Alice and Bob each think both to go > neither to go.
| Bob | ||||
|---|---|---|---|---|
| Goes | Doesn't | |||
| Alice | Goes | 4,3 | → | 2,4 |
| ↑ | ↓ | |||
| Doesn't | 1,1 | → | 3,2 |
The diagram shows the strategy graphically. The numbers represent ranks in Alice and Bob's personal preferences, relevant for Pareto efficiency
Pareto efficiency
Pareto efficiency, or Pareto optimality, is a concept in economics with applications in engineering and social sciences. The term is named after Vilfredo Pareto, an Italian economist who used the concept in his studies of economic efficiency and income distribution.Given an initial allocation of...
(thus, either 4,3 or 2,4 is better than 1,1 and 4,3 is better than 3,2 – making 4,3 and 2,4 the two solutions). The arrows represent transitions suggested by the individual preferences over which each has liberty, clearly leading to the solution for neither to go.
Liberalism and externalities
The example shows that liberalism and Pareto-efficiency cannot always be attained at the same time. Hence, if liberalism exists in just a rather constrained way, then Pareto-inefficiency could arise. Note that this is not always the case. For instance if one individual makes use of her liberal right to decide between two alternatives, chooses one of them and society would also prefer this alternative, no problem arises.Nevertheless, the general case will be that there are some externalities
Externality
In economics, an externality is a cost or benefit, not transmitted through prices, incurred by a party who did not agree to the action causing the cost or benefit...
. For instance, one individual is free to go to work by car or by bicycle. If the individual takes the car and drives to work, whereas society wants him to go to work by bicycle there will be an externality. However, no one can force the other to prefer cycling. So, one implication of Sen's paradox is that these externalities will exist wherever liberalism exists.
Ways out of the paradox
There are several ways to resolve the paradox.- First, the way Sen preferred, the individuals may decide simply to "respect" each other's choice by constraining their own choice. Assume that individual A orders three alternatives (x, y, z) according to x P y P z and individual B orders the same alternative according to z P x P y: according to the above reasoning, it will be impossible to achieve a Pareto-efficient outcome. But, if A refuses to decide over z and B refuses to decide over x, then for A follows x P y (x is chosen), and for B z P y (z is chosen). Hence A chooses x and respects that B chooses z; B chooses z and respects that A chooses x. So, the Pareto-efficient solution can be reached, if A and B constrain themselves and accept the freedom of the other player.
- A second way out of the paradox draws from game theory by assuming that individuals A and B pursue self-interested actions, when they decide over alternatives or pairs of alternatives. Hence, the collective outcome will be Pareto-inferior as the prisoner's dilemmaPrisoner's dilemmaThe prisoner’s dilemma is a canonical example of a game, analyzed in game theory that shows why two individuals might not cooperate, even if it appears that it is in their best interest to do so. It was originally framed by Merrill Flood and Melvin Dresher working at RAND in 1950. Albert W...
predicts. The way out (except Tit for tatTit for tatTit for tat is an English saying meaning "equivalent retaliation". It is also a highly effective strategy in game theory for the iterated prisoner's dilemma. It was first introduced by Anatol Rapoport in Robert Axelrod's two tournaments, held around 1980. An agent using this strategy will initially...
) will be to sign a contract, so trading away one's right to act selfishly and get the other's right to act selfishly in return. - A third possibility starts with assuming that again A and B have different preferences towards four states of the world, w, x, y, and z. A's preferences are given by w P x P y P z; B's preferences are given by y P z P w P x. Now, liberalism implies that each individual is a dictator in a least one social area. Hence, A and B should be allowed to decide at least over one pair of alternatives. For A, the "best" pair will be (w,z), because w is most preferred and z is least preferred. Hence A can decide that w is chosen and at the same time make sure that z is not chosen. For B, the same applies and implies, that B would most preferably decide between y and x. Furthermore assume that A is not free to decide (w,z), but has to choose between y and x. Then A will choose x. Conversely, B is just allowed to choose between w and z and eventually will rest with z. The collective outcome will be (x,z), which is Pareto-inferior. Hence again A and B can make each other better off by employing a contract and trading away their right to decide over (x,y) and (w,z). The contract makes sure that A decides between w and z and chooses w. B decides between (x,y) and chooses y. The collective outcome will be (w,y), the Pareto-optimal result.
Taken all together all three ways do not resolve the paradox as such. But, they answer the question: What can society do, if the paradox applies and no corresponding social decision function can handle the trade off between Pareto-optimality and liberalism? One sees that mutual acceptance and self-constraints or even contracts to trade away actions or rights are needed.