Lemniscatic elliptic function
Encyclopedia
In mathematics
, and in particular the study of Weierstrass elliptic functions, the lemniscatic case occurs when the Weierstrass invariants satisfy g2=1 and g3=0. This page follows the terminology of Abramowitz and Stegun
; see also the equianharmonic
case.
In the lemniscatic case, the minimal half period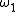
is real and equal to
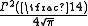
where
is the Gamma function
. The second smallest half period is pure imaginary
and equal to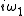
. In more algebraic terms, the period lattice is a real multiple of the Gaussian integer
s.
The constant
s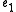
, 
and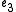 
are given by
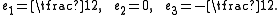
The case g2=a, g3=0 may be handled by a scaling transformation. However, this may involve complex numbers. If it is desired to remain within real numbers, there are two cases to consider: a>0 and a<0.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, and in particular the study of Weierstrass elliptic functions, the lemniscatic case occurs when the Weierstrass invariants satisfy g2=1 and g3=0. This page follows the terminology of Abramowitz and Stegun
Abramowitz and Stegun
Abramowitz and Stegun is the informal name of a mathematical reference work edited by Milton Abramowitz and Irene Stegun of the U.S. National Bureau of Standards...
; see also the equianharmonic
Equianharmonic
In mathematics, and in particular the study of Weierstrass elliptic functions, the equianharmonic case occurs when the Weierstrass invariants satisfy g_2=0 and g_3=1;This page follows the terminology of Abramowitz and Stegun; see also the lemniscatic case...
case.
In the lemniscatic case, the minimal half period
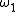is real and equal to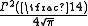where
is the Gamma functionGamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
. The second smallest half period is pure imaginary
and equal to
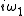. In more algebraic terms, the period lattice is a real multiple of the Gaussian integerGaussian integer
In number theory, a Gaussian integer is a complex number whose real and imaginary part are both integers. The Gaussian integers, with ordinary addition and multiplication of complex numbers, form an integral domain, usually written as Z[i]. The Gaussian integers are a special case of the quadratic...
s.
The constant
Mathematical constant
A mathematical constant is a special number, usually a real number, that is "significantly interesting in some way". Constants arise in many different areas of mathematics, with constants such as and occurring in such diverse contexts as geometry, number theory and calculus.What it means for a...
s
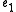, and 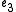are given by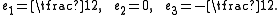The case g2=a, g3=0 may be handled by a scaling transformation. However, this may involve complex numbers. If it is desired to remain within real numbers, there are two cases to consider: a>0 and a<0.